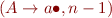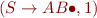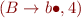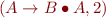Homework 5
Due Monday, November 14th, 10:10am.
Problem 1
Consider the following grammar.
S -> UT | V "Int" | "Int" T -> V "Int" | "Int" U -> S "=>" V -> T ","
Consider the input to be “Int , Int ⇒ Int”.
- Construct the CYK parsing table. Recall that each entry
 of the CYK parsing table contains those non-terminals, that can be expanded to the word
of the CYK parsing table contains those non-terminals, that can be expanded to the word 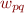 , i.e. the word from position
, i.e. the word from position  to
to  , included.
, included. - Is the grammar ambiguous for the input?
Problem 2
Consider a productive grammar in Chomsky normal form which does not contain  , i.e. the grammar does not contain unproductive rules.
, i.e. the grammar does not contain unproductive rules.
Assume the input consists of exactly  tokens, i.e., the lexical analyzer returns
tokens, i.e., the lexical analyzer returns  tokens before hitting the EOF.
tokens before hitting the EOF.
a) Assume there are  productions of form A → BC and
productions of form A → BC and  productions are of form A → a. By considering all the combinations of possible dot positions in the right-hand-side of a production and all different possible values of an item, compute the number of possible items.
productions are of form A → a. By considering all the combinations of possible dot positions in the right-hand-side of a production and all different possible values of an item, compute the number of possible items.
Recall that an item is a tuple (X, p) where X is a dotted production and p the starting position.
b) Now consider the following grammar.
S -> AB A -> BA A -> a B -> b
Determine which of the following items are possible and which are impossible during the parsing of an input with an Earley parser.
Problem 3
Consider the following grammar:
E ::= E+E E ::= E*E E ::= E=E E ::= Num | true | false
where Num represents integers.
a) Run Earley's parsing algorithm on the following input: 1=2*3=true. Give all the sets of items 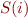 that the parser computes.
that the parser computes.
b) How many parse trees do you obtain?
c) Write down those parse trees that are correct according to the following types:
+ : Int x Int→Int
* : Int x Int→Int
= : Bool x Bool → Bool
= : Int x Int → Bool
Problem 4
Consider the following class:
class Rectangle {
var width: Int
var height: Int
var xPos: Int
var yPos: Int
def area: Int = {
if(width > 0 && height > 0)
width * height
else
0
}
def resize(maxSize: Int) {
while(area > maxSize) {
width = width / 2
height = height / 2
}
}
}
a) Determine the environment of this class.
b) By giving the type derivation trees for each method show that this class type checks.
Problem 5
Determine if the following piece of codes type check according to the type rules.
Show all steps and give type derivation trees where applicable.
a) The class Array has a field length in which the length of the array is stored.
def swap(lst: Array[Int], a: Int, b: Int): Array[Int] = {
if (a >= lst.length || b >= lst.length) lst else {
val swap = lst(a)
lst(a) = lst(b)
lst(b) = swap
lst
}
}
b)
Recall that we have the two type rules:
- If
 is a declared subclass of
is a declared subclass of  , then
, then 
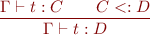
i) Give the type rule corresponding to new.
ii) Show this code typechecks.
class Shape
class Rectangle(width: Int, length: Int) extends Shape {
def area : Int = width * length
}
class Square(length: Int) extends Rectangle(length,length)
new Square(5).area