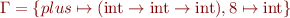LARA

Simple Types for Lambda Calculus

There are several type systems for lambda calculus

We consider here the simplest one

  • types are disjoint
  • only primitive and function types
  • every lambda binding specifies its type

Type Rules for Simply Typed Lambda Calculus

Environment $\Gamma$ maps variable names to types

Variable

\begin{equation*} \frac{(x \mapsto T) \in \Gamma} {\Gamma \vdash x : T} \end{equation*}

Application

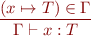
\begin{equation*} \frac{\Gamma \vdash f : T_1 \to T_2,\ e : T_1} {\Gamma \vdash (f\, e) : T_2} \end{equation*}

Abstraction

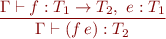
\begin{equation*} \frac{\Gamma \oplus \{x \mapsto T_1\} \vdash e : T_2} {\Gamma \vdash (\lambda x:T_1.e) : T_1 \to T_2} \end{equation*}

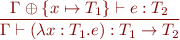
Example Primitive Operations

Among the primitive operations we consider 

plus : int -> int -> int
ite  : bool -> int -> int

Example: Type check the lambda expression

\begin{equation*} (\lambda f : \mbox{int}\to\mbox{int}.\ \lambda x : \mbox{int}.\ f(f\ x)))\ \ (plus\ 8) \end{equation*}

in environment $\Gamma = \{ {plus} \mapsto (\mbox{int} \to \mbox{int} \to \mbox{int}), 8 \mapsto \mbox{int} \}$