Earley Parser
What is Earley Parser
A parser for context-free grammars
- works for arbitrary (even ambiguous) context-free grammars
- driven by the input stream and start symbol
- uses the well-known technique of dynamic programming (avoids unnecessary computation)
- runs in O(n^3) in general
- for unambiguous grammars it runs in O(n^2)
- for grammars handled by LR parsers (we will see those later), it runs in O(n)
Items in Earley Parser
Earley parser uses grammar rules extended with exactly one 'dot' inserted, indicating the point reached by parser so far.
Call this a 'dotted production'.
Consider an example grammar rule X::=UVW. There are 4 dotted productions for this rule:
X::=.UVW X::=U.VW X::=UV.W X::=UVW.
Another example: for the grammar production
assignment ::= ID ":=" expression ";"
we have the follownig dotted productions:
assignment ::= . ID ":=" expression ";" assignment ::= ID . ":=" expression ";" assignment ::= ID ":=" . expression ";" assignment ::= ID ":=" expression . ";" assignment ::= ID ":=" expression ";" .
For each of the positions j in the input string, Earley parser stores items (called states by Earley), which are pairs of
- dotted right-hand side (e.g. X::=UV.W)
- starting position i
If e.g. the item (X::=UV.W, i) is in the set S(j), then it should be possible to parse the substring of input from position i to position j using the sequence of symbols UV.
Earley Parsing Idea
Input string: 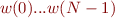 EOF
EOF
Parser examines input left to right, computes 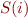 for i from 0 to N-1
for i from 0 to N-1
If D is start symbol in the original grammar, we add extra production
D'::=D EOF
and make D' start state, so parser can detect end of input.
Let  denote sequences of terminals and non-terminals of grammar.
denote sequences of terminals and non-terminals of grammar.
Goal: 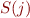 should contain all items that could appear in parsing of strings beginning with
should contain all items that could appear in parsing of strings beginning with 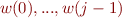
More precisely: 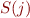 contains those items
contains those items 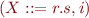 for
for  , such that for some
, such that for some 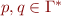

 is a grammar rule,
is a grammar rule, 
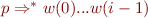
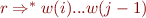
We sketch these conditions as follows:
w(0) ... w(i-1) w(i) ... w(j-1) w(j) ... w(N-1)
| | ^
| p | r | s? | |
| parser position
| X? | q? |
For 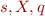 the parser did not check yet whether they agree with the input string.
the parser did not check yet whether they agree with the input string.
Steps of Early Parsing Algorithm
Initially, let 
When scanning input at position j, parser does the following operations (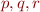 are sequences of terminals and non-terminals):
are sequences of terminals and non-terminals):
Prediction
If 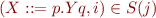 and
and  is a grammar rule, then
is a grammar rule, then
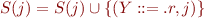
Scanning
If 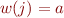 and
and 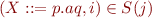 then (we can skip a):
then (we can skip a):
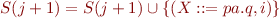
Completion
If 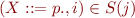 and
and 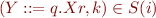 then
then
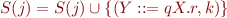
sketch of completion:
w(0) ... w(k) ... w(i) ... w(j)
| q | p |
Y::=q.Xr X::=p.
Y::=qX.r
After finishing all steps that are possible for 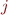 , the parser moves to
, the parser moves to  .
.
Remarks on Complexity
We measure parsing time as a function of input length N, for a fixed grammar.
- fixed number of dotted rules
In S(j) there can be at most j copies of each dotted rule (for all possible start positions)
- prediction and scanning take O(N)
- completion can take O(N^2) (but size of result still O(N))
Summing up work over all S(j), we get O(N^3)
For un-ambiguous grammar, completion is proportional to its result, so it is O(N)
- overall parsing time is O(N^2)
- becomes O(N) if |S(j)| is independent of N (bounded-state grammars)
- if number of previous points in input to examine is bounded by constant