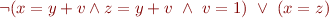Using automata to decide Presburger arithmetic
Minimalistic syntax for Presburger arithmetic is given by the following grammar:
F ::= V=1 | V=V | V=V+V |  F | F
F | F  F |
F |  v. F
v. F
V ::= v_1 | v_2 | …
Variables range over non-negative integers.
Example formula: 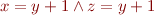
This is no loss of generality because we can express all other constructs using the given ones:
- integers are equivalence classes of pairs of non-negative integers, replacing
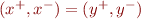 with
with  , and expressing
, and expressing  as
as  .
. - arbitrary additive constants: use binary notation and the addition operator and
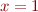 operator
operator - multiplication by constant
 : use addition, also binary development of
: use addition, also binary development of 
 is
is 
 divides
divides  is
is 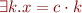
- propositional operations: use

 : use
: use 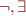
Automata for Presburger Arithmetic Formulas
Automaton for formula:  accepts certain strings in alphabet
accepts certain strings in alphabet 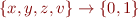 . An example string that this automaton accepts can be represented as follows:
. An example string that this automaton accepts can be represented as follows:
x: 0 0 1 0 0 y: 1 1 0 0 0 z: 0 0 1 0 0 v: 1 0 0 0 0
This string represents the satisfying assignment 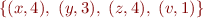 for the above formula. If we take the valid formula
for the above formula. If we take the valid formula
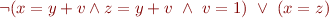
the corresponding automaton accepts all strings. (End of example.)
Consider a formula  in this minimal syntax. Rename all bound variables to be mutually distinct and distinct from free variables. Let these variables be
in this minimal syntax. Rename all bound variables to be mutually distinct and distinct from free variables. Let these variables be  . For every subformulas
. For every subformulas  of
of  we construct an automaton
we construct an automaton 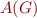 whose alphabet is
whose alphabet is 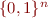 . This automaton will accept strings (elements of
. This automaton will accept strings (elements of 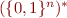 that encode
that encode  -tuples of integers for which
-tuples of integers for which  is true. The automaton
is true. The automaton 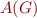 simultaneously reads the bits of binary representations of all
simultaneously reads the bits of binary representations of all  variables at once.
variables at once.
If 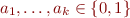 , let
, let  . That is,
. That is, 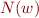 denotes the value of the string
denotes the value of the string  viewed as a binary representation of a non-negative integer. We will define
viewed as a binary representation of a non-negative integer. We will define 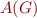 such that for every
such that for every  and every matrix
and every matrix 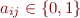 ,
, 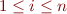 and
and 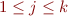 , the following correspondence holds:
, the following correspondence holds:
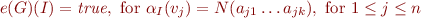
iff
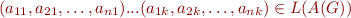
Graphically:
a11 ... a1k ---> v1 a21 ... a2k ---> v2 ... ... ... ... an1 ... ank ---> vn ^ | L(G)
In matrix  , row
, row  gives the value for variable
gives the value for variable  , whereas column
, whereas column 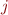 gives the
gives the 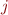 -th symbol of the input word for the automaton.
-th symbol of the input word for the automaton.
Case 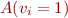
The automaton expects to see as the first symbol some 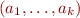 with
with  , if it finds it, it goes into accept state. If it ever encounters another symbol with
, if it finds it, it goes into accept state. If it ever encounters another symbol with  , then it goes into an error state.
, then it goes into an error state.
Case 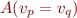
The automaton expects to see a sequence of symbols 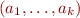 with
with 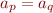 and transitions into an error state if a different symbol occurs.
and transitions into an error state if a different symbol occurs.
Case 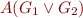 ,
, 
This follows from closure properties of finite state machines, take automata that denote union and complement of the languages.
Case 
(Sketch) This is projection operation on an automaton. Take 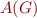 and replace each transition with label
and replace each transition with label 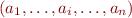 with two transitions
with two transitions 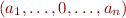 and
and 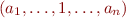 into the same destination state. The ideas is that existentially quantifying over an integer is similar to existentially quantifying over all of its bits. There are some subtleties that have to do with the length of the existentially quantified variables; we explain this when we give the more general construction for Weak Monadic Logic of One Successor.
into the same destination state. The ideas is that existentially quantifying over an integer is similar to existentially quantifying over all of its bits. There are some subtleties that have to do with the length of the existentially quantified variables; we explain this when we give the more general construction for Weak Monadic Logic of One Successor.
Why the correspondence implies decidability. Consider a PA formula  . The following are equivalent:
. The following are equivalent:
 is satisfiable
is satisfiable- there exist some interpretation of free variables of
 such that
such that 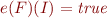
- there exist some digits
 such that
such that 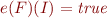 for
for 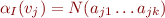
- there exist some digits
 such that
such that 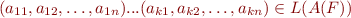
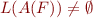
 has a reachable accepting state
has a reachable accepting state
Therefore, to check if  is satisfiable, we construct
is satisfiable, we construct 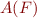 automaton and check whether the graph of
automaton and check whether the graph of 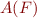 has a reachable accepting state.
has a reachable accepting state.
Example: Step-by-step construction of automaton for