Using Automata to Decide WS1S
Consider a formula  of WS1S. Let
of WS1S. Let  be a finite set of all variables in
be a finite set of all variables in  . We construct an automaton
. We construct an automaton 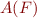 in the finite alphabet
in the finite alphabet
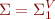
for 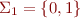 such that the following property holds: for every
such that the following property holds: for every  ,
,
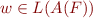 iff
iff 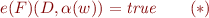
where 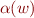 is an interpretation of WS1S (mapping variables
is an interpretation of WS1S (mapping variables  to finite sets) defined by
to finite sets) defined by
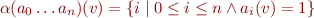
Instead of  we write for short
we write for short  . So, we design automata so that:
. So, we design automata so that:

The following lemma follows from the definition of semantic evaluation function 'e' and the shorthand  .
.
Lemma: Let 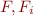 denote formulas,
denote formulas,  . Then
. Then
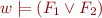 iff
iff  or
or 
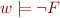 iff
iff 
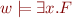 iff
iff 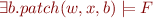
.......
....... 0
.......
bbbbbbbbbbbbbb
.......
....... 0
.......
_______
w
______________
patch(w,x,b)
Let 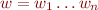 where
where  and
and  where
where  .
Let
.
Let  . Define
. Define 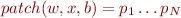 where
where  such that
such that
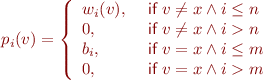
We define the automaton by recursion on the structure of formula.
Case 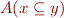 :
:
Case 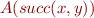 :
:
Case 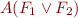 :
:
Case  :
:
Example: Use the rules above to compute (and minimize) the automaton for 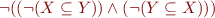 .
.
Proof of correctness if by induction. For example, for disjunction we have:
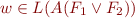
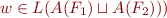
 , so by I.H.
, so by I.H. , so by Lemma above,
, so by Lemma above,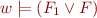
Existential Quantification
Case  :
:
To maintain the equivalence  above, we need that for every word,
above, we need that for every word,
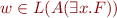
iff

Given a deterministic automaton 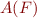 , we can construct a deterministic automaton
accepting
, we can construct a deterministic automaton
accepting 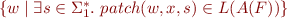 in two steps:
in two steps:
- take the same initial state
- for each transition
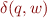 introduce transitions
introduce transitions ![Math $\delta(q,w[x:=b])$](/w/lib/exe/fetch.php?media=wiki:latex:/img637d7f965b5884a03265e9cf07dc4a5e.png) for all
for all 
- initially set final states as in the original automaton
- if
 is a final state and
is a final state and  is such that
is such that 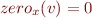 for all
for all 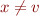 , and if
, and if 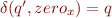 , then set
, then set  also to be final
also to be final
Example 1: Compute automaton for formula 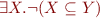 . MONA syntax:
. MONA syntax:
var2 Y; ex2 X: ~(X sub Y);
Command to produce dot file:
mona -gw $1 | dot -Tps > output.ps
Example 2: Compute automaton for formula 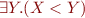 where
where  is interpreted treating
is interpreted treating  as digits of natural numbers. Also compute the automaton for the formula
as digits of natural numbers. Also compute the automaton for the formula 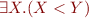 .
.
Define less-than relation in MONA and encode this example.
References
- MONA tool manual (Chapter 3, page 18)
![Math $[x \rightarrow y]^*$](/w/lib/exe/fetch.php?media=wiki:latex:/imgbca03e449a578f249987bb15c16e0500.png)
![Math $[\lnot x \land \lnot y]^* [x \land \lnot y][\lnot x \land y] [\lnot x \land \lnot y]^*$](/w/lib/exe/fetch.php?media=wiki:latex:/img001b59fd48ab63cda68914a054be43fe.png)

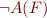 .
.