Using automata to decide MSOL over strings
Compare this to Using automata to decide Presburger arithmetic.
We will define 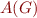 such that for every
such that for every  and for all
and for all  , for every matrix
, for every matrix 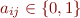 where for
where for 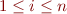 and
and 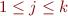 ,
,
![Equation \begin{equation*}
[\![G]\!] [v_i \mapsto \{j \mid a_{ij}=1 \}]_{i=1}^n = \mbox{true}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgb2d06c486fc7160c7ac55aa5eacf5d34.png)
iff
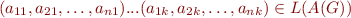
a11 ... a1k ---> v1 a21 ... a2k ---> v2 ... ... ... ... an1 ... ank ---> vn ^ | L(G)
In matrix  , row
, row  gives the set for variable
gives the set for variable  , whereas column
, whereas column 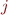 gives the
gives the  -th symbol of the input word for the automaton.
-th symbol of the input word for the automaton.
Case 
The automaton checks that every input symbol is suchj that if  then also
then also 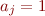 . If it ever encounters a different symbol, it goes into an error state.
. If it ever encounters a different symbol, it goes into an error state.
Case 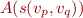
The automaton expects to see first a sequence of symbols 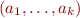 such that
such that 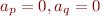 , then a symbol with
, then a symbol with 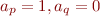 followed by a symbol with
followed by a symbol with 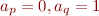 , followed again by a sequence with
, followed again by a sequence with 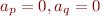 .
.
Case 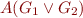 ,
, 
This follows from closure properties of finite state machines, take automata that denote union and complement of the languages.
Case 
This is projection operation on an automaton. Take 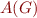 and replace each transition with label
and replace each transition with label 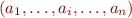 with two transitions
with two transitions 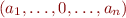 and
and 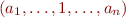 into the same destination state. This is because existentially quantifying over an integer is the same as existentially quantifying over all of its bits.
into the same destination state. This is because existentially quantifying over an integer is the same as existentially quantifying over all of its bits.
NOTE: What if the witness is longer than  ?
?
- concatenate the language of strings of the form
![Math $[\bigwedge_{j=1,j\neq i}^n \lnot v_j]*$](/w/lib/exe/fetch.php?media=wiki:latex:/img18721010ba3738ed72f1d19468847a3d.png) to the language of the automaton
to the language of the automaton - there exists
 so that equivalence holds for all
so that equivalence holds for all 
As in the case of Presbuger arithmetic, to check if  is satisfiable, we construct
is satisfiable, we construct 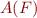 as a deterministic automaton and check whether the graph of
as a deterministic automaton and check whether the graph of 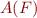 has a reachable accepting state.
has a reachable accepting state.
Complexity
The above construction determinizes automaton whenever it needs to perform negation. Moreover, existential quantifier forces the automaton to be non-deterministic. Therefore, with every alternation between  and
and  we obtain an exponential blowup. For formula with n alternations we have
we obtain an exponential blowup. For formula with n alternations we have  complexity with a stack of exponentials of height
complexity with a stack of exponentials of height  . Is there a better algorithm? The following paper shows that, in the worst case such behavior cannot be avoided, because of such high expressive power of MSOL over strings.
. Is there a better algorithm? The following paper shows that, in the worst case such behavior cannot be avoided, because of such high expressive power of MSOL over strings.
- Cosmological Lower Bound on the Circuit Complexity of a Small Problem in Logic (See the introduction and the conclusion sections)
- circuit versus assymptotic time complexity (uniformity, specific instance versus assymptotic bound)
- the density question
- do we need to know how to check validity for all MSOL formulas