Tree automata
Finite Automata as Automata in Unary Language
Consider a finite alphabet  . A word
. A word  is a finite sequence of symbols from
is a finite sequence of symbols from  .
.
We can represent such a sequence as a term, as follows
- treat elements of
 as unary function symbols
as unary function symbols - let
 be a constant symbol
be a constant symbol
Represent 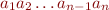 as a ground term
as a ground term
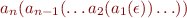
We define the notion of finite state machine as accepting a set of such terms.
Bottom up tree automata
Definition:Given an alphabet  , a non-deterministic bottom-up tree automaton in language
, a non-deterministic bottom-up tree automaton in language  is
is 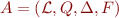 where
where
 is a set of states
is a set of states is the set of final states
is the set of final states is a set of rewrite rules
is a set of rewrite rules
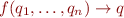
where  is a function symbol of arity
is a function symbol of arity  and where
and where 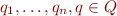 .
.
Note: In the case of constant  the transition has the form
the transition has the form  and specifies possible initial states.
and specifies possible initial states.
A ground term in language  is accepted by the automaton iff it is possible to reach
is accepted by the automaton iff it is possible to reach  by apply rewrite rules in
by apply rewrite rules in  to term
to term  .
.
This rewriting process is a sequence of transitions  where
where 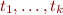 are terms in language
are terms in language  with
with  being treated as constants of arity zero.
being treated as constants of arity zero.
Definition: A regular tree language is a set of terms accepted by a non-deterministic bottom-up tree automaton.
Example:
- bottom up tree automaton accepting trees with an even number of nodes in the tree, in alphabet with constant 'a', binary function 'f'.
- bottom up tree automaton accepting expressions with complement, union, intersection; accepting only expressions that are monotonic in each variable
Non-deterministic top-down tree automaton: reverse a bottom-up tree automaton
Deterministic top-down tree automaton: more restrictive. Is there deterministic automaton to check the parity of the number of nodes?
Closure Properties of Tree Automata
Definition: We say bottom-up tree automaton is deterministic iff for every  of arity
of arity  and
and 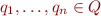 there exists exactly one
there exists exactly one  such that
such that 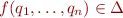 .
.
Lemma: For every bottom up tree automaton there exists a deterministic bottom up tree automaton accepting the same language.
Closure under:
- union
- negation
- intersection
Comparison to context-free grammars: closure under intersection and complement. Parser trees are regular, their yield is not.
Projection.
Weak Monadic Logic of Two Successors (WS2S)
We generalize Weak Monadic Logic of One Successor to logic that allows quantification over finite subsets of an infinite binary tree.
- a finite subset
 of nodes in an infinite binary tree can be specified by listing, for each node in
of nodes in an infinite binary tree can be specified by listing, for each node in  , a path in the binary that leads to this node
, a path in the binary that leads to this node - a path in a binary tree is a finite sequence of “left” and “right” moves from the root
- we encode each node as a string
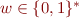
The domain  of WS2S is the set of all finite subsets
of WS2S is the set of all finite subsets 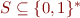 .
.
Minimalistic syntax:
We consider interpretations 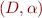 where
where
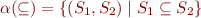
where  takes a tree node and finds its left child:
takes a tree node and finds its left child:
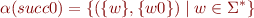
and where  takes a tree node and finds its right child:
takes a tree node and finds its right child:
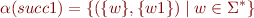
The meaning of formulas is then given by standard First-order logic semantics.
Deciding WS2S
A construction is similar to one for WS1S and is possible thanks to closure properties of finite automata.
Examples:
- subset
- successor
Verification of Trees
Infinite Trees
S2S (without restriction to finite sets) is also decidable. The proofs are much more complex:
- cannot use bottom-up automata
- complementation is difficult
Key reference: