Using Galois Connection
Terminology:
 - concrete domain
- concrete domain - abstract domain
- abstract domain - concretization function
- concretization function - abstraction function
- abstraction function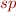 - (the usual) strongest postcondition (or just “strongest post”)
- (the usual) strongest postcondition (or just “strongest post”) - abstract post, abstract transformer (transforms one abstract element into another)
- abstract post, abstract transformer (transforms one abstract element into another)
Abstraction function for sign analysis.
Define  using
using  and
and  :
:
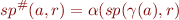
Best Abstract Transformer
 can in general be arbitrarily imprecise while preserving correctness.
can in general be arbitrarily imprecise while preserving correctness.
Given  , we would like
, we would like  to be as precise as possible while being correct.
to be as precise as possible while being correct.
The most precise  is called “best abstract transformer”.
is called “best abstract transformer”.
If 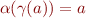 , then
, then  defined using
defined using  and
and  is the most precise one (given the abstract domain and particular blocks in the control-flow graph).
is the most precise one (given the abstract domain and particular blocks in the control-flow graph).