Model Checking Systems with Procedures
Suppose we have a system given by a context-free grammar  and a specification given by a regular language
and a specification given by a regular language  .
.
System meets the specification iff  , that is
, that is
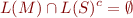
Note:
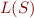 is a regular language
is a regular language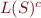 is also a regular language
is also a regular language- intersection of a context-free and regular language is a context-free language (and we can compute a grammar for it)
- it is decidable to check if a given grammar is empty
Recall how the intersection of context-free and regular language works:
- create a pushdown automaton for the context-free language
- create a finite state automaton for the regular language
- apply product construction: finite control is as in intersection of regular languages, stack is as in the original pushdown automaton
Next: a direct approach that combines the above individual constructions into one