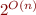Syntactic Rules for Hoare Logic

Summary of Proof Rules

We next present (one possible) summary of proof rules for Hoare logic.

Weakening and Strengthening

Strengthening precondition:

$\begin{equation*} \frac{\models P_1 \rightarrow P_2 \ \ \ \{P_2\}c\{Q\}} {\{P_1\}c\{Q\}} \end{equation*}$

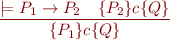
Weakening postcondition:

$\begin{equation*} \frac{\{P\}c\{Q_1\} \ \ \ \models Q_1 \rightarrow Q_2} {\{P\}c\{Q_2\}} \end{equation*}$

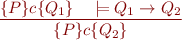
Loop Free Blocks

We can directly use rules we derived for basic loop-free code. Either through weakest preconditions or strongest postconditions.

$\begin{equation*} \{wp(c,Q)\} c \{Q\} \end{equation*}$

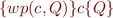
or,

$\begin{equation*} \{P\} c \{sp(P,c)\} \end{equation*}$

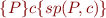
For example, we have:

$\begin{equation*}\begin{array}{l} \{Q[x:=e]\}\ (x=e)\ \{Q\} \\ \ \\ \{\forall x.Q\}\ {\it havoc}(x)\ \{Q\} \\ \ \\ \{P\}\ assume(F)\ \{P \land F\} \end{array} \end{equation*}$

Loops

$\begin{equation*} \frac{\{I\}c\{I\}} {\{I\}\ {\it l{}o{}o{}p}(c)\ \{I\}} \end{equation*}$

Sequential Composition

$\begin{equation*} \frac{\{P\}\, c_1 \{Q\} \ \ \ \{Q\}\, c_2\, \{R\}} {\{P\}\ c_1;c_2\ \{R\}} \end{equation*}$

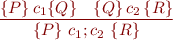
Non-Deterministic Choice

$\begin{equation*} \frac{\{P\} c_1 \{Q\} \ \ \ \{P\} c_2 \{Q\}} {\{P\} c_1 [] c_2 \{Q\}} \end{equation*}$

While Loops

Knowing that the while loop:

while (F) c;

is equivalent to:

loop (assume(F); c); 
assume(not F);

It follows that the rule for while loops is:

$\begin{equation*} \frac{(\models P \rightarrow I);\ \{I \wedge F \}c\{I\};\ (\models (I \land \lnot F) \rightarrow Q))} {\{P\}\ {\it while}\{I\}(F)(c)\ \{Q\}} \end{equation*}$

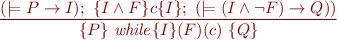
Applying Proof Rules given Invariants

Let us treat 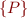$\{P\}$ as a new kind of statement, written

assert(P)

For the moment the purpose of assert is just to indicate preconditions and postconditions. When we write

assert(P)
c1;
assert(Q)
c2;
assert(R)

we expect that these Hoare triples hold:

{P} c1 {Q}
{Q} c2 {R}

Consider control-flow graph of a program with statements assert,assume,x=e and with graph edges expressing “[]” and “;”.

We will say that the program $c$ is sufficiently annotated iff

the first statement is assert(Pre)
the last statement is assert(Post)
every cycle in the control-flow graph contains at least one assert

An assertion path is a path in its control-flow graph that starts and ends with assert. Given assertion path

assert(P)
c1
...
cK
assert(Q)

we omit any assert statements in the middle, obtaining from c1,…,cK statements d1,…,dL. We call

$\begin{equation*} \{P\} d1\ ;\ \ldots\ ;\ dL \{Q\} \end{equation*}$

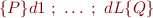
the Hoare triple of the assertion path.

A basic path is an assertion path that contains no assert commands other than those at the beginning and end. Each sufficiently annotated program has finitely many basic paths.

Theorem: If Hoare triple for each basic path is valid, then the Hoare triple 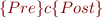$\{Pre\}c\{Post\}$ is valid.

Proof: If each basic path is valid, then each path is valid, by induction and Hoare logic rule for sequential composition. Each program is union of (potentially infinitely many) paths, so the property holds for the entire program. (Another explanation: consider any given execution and corresponding path in the control-flow graph. By induction on the length of the path we prove that all assert statements hold, up to the last one.)

The verification condition of a basic path is the formula whose validity expresses the validity of the Hoare triple for this path.

Simple verification conditions for a sufficiently annotated program is the set of verification conditions for each each basic path of the program.

One approach to verification condition generation is therefore:

start with sufficiently annotated program
generate simple verification conditions
prove each of the simple verification conditions

In a program of size $n$ , what is the bound on the number of basic paths? it can be $2^{O(n)}$

Remedies:

require more annotations (e.g. at each merge point)
- extreme case: assertion on each CFG vertex - this gives classical Hoare logic proof
merge subgraphs without annotations, as in Lecture 03: perform sequential composition and disjunction of formulas on edges
generate correctness formulas for multiple paths in an acyclic subgraph at once, using propositional variables to encode the existence of paths

LARA