Variable Range Analysis for Example Program
The general form of abstract interpretation of the collecting semantics is analogous to collecting semantics, but replaces operations on sets with operations on the lattice:
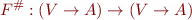
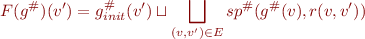
Here  will be
will be  except at the entry into our control-flow graph, where it approximates the set of initial states at the entry point.
except at the entry into our control-flow graph, where it approximates the set of initial states at the entry point.
Abstract Analysis Domain
In Collecting Semantics for Example Program we had representation for all possible sets of states:

Here we have representation of only certain states, namely intervals:
![Equation \begin{equation*}
A =
\begin{array}[t]{l}
\{ \bot \}\ \cup \\
\{(-\infty,q] \mid q \in \mathbb{Z} \} \cup \\
\{[p,+\infty) \mid p \in \mathbb{Z} \} \cup \\
\{[p,q] \mid p \le q \} \cup \\
\{ \top \}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imga55d01a1214a216061739c019c550466.png)
The meaning of domain elements is given by a monotonic concretization function 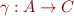 :
:
![Equation \begin{equation*}
\begin{array}[t]{rcl}
\gamma(\bot) &=& \emptyset \\
\gamma(\{(-\infty,q]) &=& \{ x \mid x \le q\} \\
\gamma(\{[p,+\infty)) &=& \{x \mid p \le x \} \\
\gamma(\{[p,q]) &=& \{x \mid p \le x \land x \le q \} \\
\gamma(\top) &=& \mathbb{Z}
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imga10d29c5093a7d942b5666aedd594949.png)
From monotonicity and  it follows
it follows
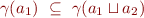
and thus
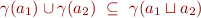
We try to define  to be as small as possible while satisfying this condition.
to be as small as possible while satisfying this condition.
Define abstraction function  such that
such that
![Math $\alpha(s) = [\min s, \max s]$](/w/lib/exe/fetch.php?media=wiki:latex:/img89513132ed70b7d794223316eb0a0cca.png) if those values exist (set is bounded from below and above)
if those values exist (set is bounded from below and above) if there is lower but no upper bound
if there is lower but no upper bound![Math $\alpha(s) = (-\infty, \max s]$](/w/lib/exe/fetch.php?media=wiki:latex:/img1499d14af4639b63520f3b09612101cb.png) if there is upper but no lower bound
if there is upper but no lower bound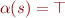 if there is no upper and no lower bound
if there is no upper and no lower bound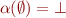
Lemma: The pair 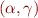 form a Galois Connection.
form a Galois Connection.
By property of Galois Connection, the condition 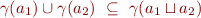 is equivalent to
is equivalent to
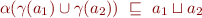
To make  as small as possible, we let the equality hold, defining
as small as possible, we let the equality hold, defining
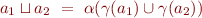
For example,
![Equation \begin{equation*}
\begin{array}{rcl}
[0,2] \sqcup [5,8]
&=& \alpha(\gamma([0,2]) \cup \gamma([5,8])) \\
&=& \alpha(\{0,1,2, 5,6,7,8\}) \\
&=& [0,8]
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img15a6b11091fc70c990bff839e694e872.png)
Abstract Postcondition
We had: 
Now we have: 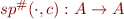
For correctness, the condition from Abstract Interpretation Recipe is that for each  and each command
and each command  :
:
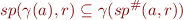
We would like  to be as small as possible so that this condition holds
to be as small as possible so that this condition holds
By property of Galois Connection, the condition 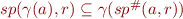 is equivalent to
is equivalent to
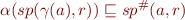
Because we want  to be as small as possible (to obtain correct result), we let equality hold:
to be as small as possible (to obtain correct result), we let equality hold:
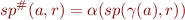
Because we know 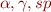 , we can compute the value of
, we can compute the value of 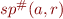 by simplifying certain expressions involving sets of states.
by simplifying certain expressions involving sets of states.
Example: for  we have:
we have:
![Equation \begin{equation*}
\begin{array}{rcl}
sp^\#([p,q],x:=x+3)
&=& \alpha(sp(\gamma([p,q]),x:=x+3)) \\
&=& \alpha(sp(\{x \mid \ p \le x \land x \le q\},x:=x+3)) \\
&=& \alpha(\{x+3 \mid p \le x \land x \le q\}) \\
&=& \alpha(\{y \mid p+3 \le y \land y \le q+3\}) \\
&=& [p+3,q+3]
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgae403c9df93b775f126adf9a652bd634.png)
For  an integer constant and
an integer constant and  , we have
, we have
![Equation \begin{equation*}
sp^\#(a,x:=K) = [K,K]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img5b40eb8e00d04612f36d10ef57e06b6d.png)
Note that for every command given by relation  , we have
, we have
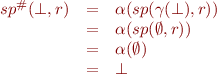
Abstract Semantic Function for the Program
Solving Abstract Function
Doing the analysis means computing 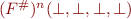 for
for  :
:
![Equation \begin{equation*}
\begin{array}{l}
(\bot,\bot,\bot,\bot) \\
(\top,\bot,\bot,\bot) \\
(\top,[0,0],\bot,\bot) \\
(\top,[0,0],[0,0],\bot) \\
(\top,[0,3],[0,3],\bot) \\
(\top,[0,3],[0,3],\bot) \\
(\top,[0,6],[0,3],\bot) \\
(\top,[0,6],[0,6],\bot) \\
(\top,[0,9],[0,9],\bot) \\
(\top,[0,12],[0,9],\bot) \\
(\top,[0,12],[0,9],[10,12]) \\
(\top,[0,12],[0,9],[10,12]) \\
\ldots
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img75e6f1f0a7a97ed3fbfbef5d47960268.png)
Note the approximation (especially in the last step) compared to Collecting Semantics for Example Program.
Correctness
We are talking about overapproximating analysis.
In Lecture 05 we discussed that a sufficient condition is to have
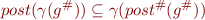
When we talk about the transition relation, then we need a big  , which maps states including program counter. We define it by
, which maps states including program counter. We define it by
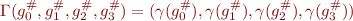
The soundness condition is then:
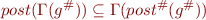
where  is defined pointwise for each component of the tuple.
By definition of
is defined pointwise for each component of the tuple.
By definition of  ,
, 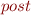 , and
, and 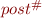 , this reduces to pointwise conditions.
, this reduces to pointwise conditions.
For example, we need to ensure that
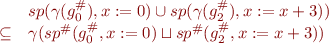
To show this, we can start from left hand side and push  outside, obtaining larger and larger sets.
outside, obtaining larger and larger sets.
Exercise 1
Consider an analysis that has two integer variables, for which we track intervals, and one boolean variable, whose value we track exactly.
Give the type of  for such program.
for such program.
Exercise 2
Consider the program that manipulates two integer variables  .
.
Consider any assignment 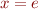 , where
, where  is a linear combination of integer variables, for example,
is a linear combination of integer variables, for example,
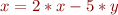
Consider an interval analysis that maps each variable to its value.
Describe an algorithm that will, given a syntax tree of 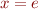 and intervals for
and intervals for  (denoted
(denoted ![Math $[a_x,b_x]$](/w/lib/exe/fetch.php?media=wiki:latex:/img5c18c4d639e16bb5e8c09403bbea16c8.png) ) and
) and  (denoted
(denoted ![Math $[a_y,b_y]$](/w/lib/exe/fetch.php?media=wiki:latex:/img760cca74ab69348a7aaf9cdcf60d5b50.png) ) find the new interval
) find the new interval ![Math $[a,b]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgfe477a2781d275b4481790690fccd15f.png) for
for  after the assignment statement.
after the assignment statement.
Exercise 3
a)
For a program whose state is one integer variable and whose abstraction is an interval, derive general transfer functions 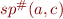 for the following statements
for the following statements  , where
, where  is an arbitrary compile-time constant known in the program:
is an arbitrary compile-time constant known in the program:
- x= K;
- x= x + K;
- assume(x ⇐ K)
- assume(x >= K)
b)
Consider a program with two integer variables, x,y. Consider analysis that stores one interval for each variable.
- Define the domain of lattice elements
 that are computed for each program point.
that are computed for each program point. - Give the definition for statement
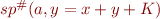
c)
Draw the control-flow graph for the following program.
// v0 x := 0; // v1 while (x < 10) { // v2 x := x + 3; } // v3 if (x >= 0) { if (x <= 15) { a[x]=7; // made sure index is within range } else { // v4 error; } } else { // v5 error; }
Run abstract interpretation that maintains an interval for  at each program point, until you reach a fixpoint.
at each program point, until you reach a fixpoint.
What are the fixpoint values at program points  and
and 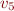 ?
?
![Equation \begin{equation*}
\begin{array}{l}
F(g_0,g_1,g_2,g_3) = \\
\begin{array}[t]{l}
(\mathbb{Z}, \\
sp(g_0, x:=0) \cup sp(g_2, x:=x+3),\\
sp(g_1, assume(x < 10)), \\
sp(g_1, assume(\lnot(x<10))))
\end{array}
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img72fbfe992fe55bd85d8c7cb45f21a0c3.png)
![Equation \begin{equation*}
\begin{array}{l}
F^\#(g^\#_0,g^\#_1,g^\#_2,g^\#_3) = \\
\begin{array}[t]{l}
(\top, \\
sp^\#(g^\#_0, x:=0) \sqcup sp^\#(g^\#_2, x:=x+3),\\
sp^\#(g^\#_1, assume(x < 10)), \\
sp^\#(g^\#_1, assume(\lnot(x<10))))
\end{array}
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img564f85363922d324fe9934ca1f80ab37.png)