Galois Connection

Constructing Partial Orders using Maps

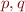Example: Let $A$ be the set of all propositional formulas containing only variables $p,q$ . For a formula 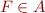$F \in A$ define

$\begin{equation*} [F] = \{ (u,v).\ u,v \in \{0,1\} \land F \mbox{ is true for } p\maptso u, q \mapsto v \} \end{equation*}$

i.e. $[F]$ denotes the set of assignments for which $F$ is true. Note that $F \implies G$ is a tautology iff $[F] \subseteq [G]$ . Define ordering on formulas $A$ by

$\begin{equation*} F \le G \iff [F] \subseteq [G] \end{equation*}$

Is $\le$ a partial order? Which laws does $\le$ satisfy? End of example.

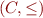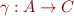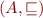Lemma: Let $(C,\le)$ be an lattice and $A$ a set. Let $\gamma : A \to C$ be an injective function. Define oder $x \sqsubseteq y$ on $A$ by $\gamma(x) \le \gamma(y)$ . Then $(A, \sqsubseteq)$ is a partial order.

Note: even if 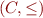$(C,\le)$ had top and bottom element and was a lattice, the constructed order need not have top and bottom or be a lattice. For example, we take $A$ to be a subset of $A$ and define $\gamma$ to be identity.

How can we ensure that we obtain a “nice” partial order?

Galois Connection

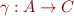Galois connection (named after Évariste Galois) is defined by two monotonic functions $\alpha : C \to A$ and $\gamma : A \to C$ between partial orders $\leq$ on $C$ and $\sqsubseteq$ on $A$ , such that

$\begin{equation*} \alpha(c) \sqsubseteq a\ \iff\ c \leq \gamma(a) \qquad (*) \end{equation*}$

for all $c$ and $a$ (intuitively, the condition means that $c$ is approximated by $a$ ).

Lemma: The condition $(*)$ holds iff the conjunction of these two conditions:

$\begin{eqnarray*} c &\leq& \gamma(\alpha(c)) \\ \alpha(\gamma(a)) &\sqsubseteq& a \end{eqnarray*}$

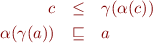
holds for all $c$ and $a$ .