Powerset of Conjunctions of Predicates
We now apply Powerdomains for Finite Domains to Abstract Interpretation with Conjunctions of Predicates.
Given the set of predicates 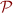 , the domain are sets of sets of predicates.
, the domain are sets of sets of predicates.
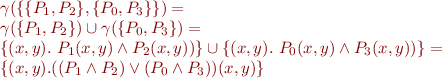
Result are disjunctions of conjunctions of predicates i.e. arbitrary boolean combinations of predicates.
This is the domain used in predicate abstraction techniques.
Even stronger domains are obtained when we allow quantified formulas. See:
- Symbolic Shape Analysis, PhD dissertation by Thomas Wies
Given a fixed number of predicates and  program points, what is
program points, what is
- the number of elements of this powerset lattice
- height of this powerset lattice
Example: 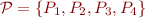 with
with
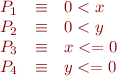
Consider this program where the initial values of x and y are arbitrary.
Compute abstraction using conjunctions of predicates, as well as disjunction of conjunctions of predicates, if we have predicates 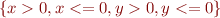 .
.
if (x > 0) { y = 1 } else { y = -1 }
Relationship to abstract reachability tree.