Powerdomains
Let 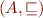 be a lattice.
be a lattice.
Define 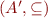 with
with  .
.
The lattice is exponentially larger, and it can be much more precise.
Example: applying powerdomain to interval lattice means that we can represent every possible set of states from concrete execution, because each element can be represented by abstract state with exact intervals.
Given 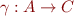 , define
, define 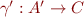 by
by
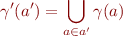
We define
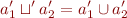
and there is no approximation in 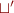 , that is,
, that is,
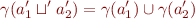
The abstraction function can be defined for each state, for  , we have
, we have 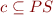 , so
, so
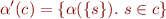
Example: Abstracting set 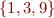 by interval gives
by interval gives
![Equation \begin{equation*}
\alpha(\{1,3,9\}) = [1,9]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img42160b44fa1829b6c53a11783d980238.png)
Abstracting it by powerset of interval gives
![Equation \begin{equation*}
\alpha'(\{1,3,9\}) = \{ \alpha(\{1\}), \alpha(\{3\}), \alpha(\{9\}) \} = \{ [1,1], [3,3], [9,9] \}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgbb81721bf04d6969836a0b7ed3014568.png)
Also, we can define
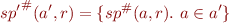
Example:
![Equation \begin{equation*}
{sp{}'}^\#(\{ [1,1], [3,3], [9,9] \}, x:=x*x) = \{ [1,1], [9,9], [81,81] \}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img8ea868b8d2c3c483d4c7b92cd9eb89f2.png)
With such large domain, widening is even more important.
A natural widening is to go back to non-power domain element:
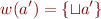
Example:
![Equation \begin{equation*}
w(\{ [1,1], [9,9], [81,81] \}) = \{ [1,81] \}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img7f10ec5ce8cca05c2c2c4f555074ba49.png)
We can also apply the standard interval widening (with “jumps”) on top of this.
So, we can get precision or efficiency, depending on the use of widening.