Abstract Interpretation with Conjunctions of Predicates
Parameters: a finite set of formulas 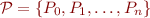 in program variables (often called predicates in this context). Suppose
in program variables (often called predicates in this context). Suppose 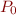 is the formula 'false'.
is the formula 'false'.
Example: 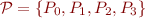 with
with
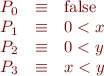
A simple description of this analysis is as the instance of the following idea: assume optimistically that all predicates hold at every program point (the conjunction of all of them holds). Then check whether the result is a sufficiently annotated program. If it is not, then remove the predicates that do not hold, and repeat this process. In the worst case we end up with no predicates holding (the top element of the lattice). There are, however, different ways of removing predicates, and this abstract interpretation formulation gives us one particular way.
Suppose for simplicity we consider as states tuples 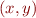 of values of integer variables
of values of integer variables  and
and  .
.
For a formula  containing variables
containing variables  and
and  and given
values
and given
values 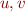 we write
we write 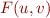 to denote the truth value of
to denote the truth value of
 in interpretation that maps
in interpretation that maps  to
to  and maps
and maps  to
to  .
(We can formally define this if we have a truth-value function that gives semantics to formulas under a given interpretation function, as in classical semantics of first-order logic.)
.
(We can formally define this if we have a truth-value function that gives semantics to formulas under a given interpretation function, as in classical semantics of first-order logic.)
Lattice
Let 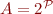 , so for
, so for  we have
we have  .
.
We design analysis using Abstract Interpretation Recipe.
Define a syntactic order on 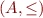 :
:

Clearly, this forms a finite lattice with height  .
.
Note that, because the order is inverted, the full set
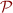 is the bottom and
is the bottom and  is the top of the
lattice.
is the top of the
lattice.
Example:
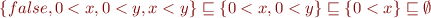
Note that  implies that the formula
implies that the formula
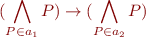
is a valid formula, because every conjunct on right-hand side appears also on the left-hand side.
- Does the converse hold?
We could also define ordering on elements of  using the above implication.
This is a pre-order. We could work with equivalence classes if we use
a theorem prover to check the equivalence of formulas.
using the above implication.
This is a pre-order. We could work with equivalence classes if we use
a theorem prover to check the equivalence of formulas.
Concretization Function Gamma
Define
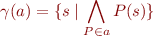
i.e. set of states in which all predicates in  evaluate to true.
evaluate to true.
Example: In our example, the definition reduces to
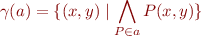
In particular, whenever  , then
, then
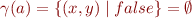
Empty conjunction is by definition true, so
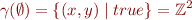
Monotonicity of Gamma
We observe that concretization is monotonic. Indeed, suppose  . Then
. Then 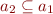 , so
, so
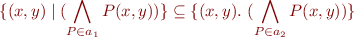
which means  .
.
Example:
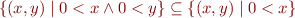
i.e. 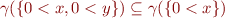 .
.
Abstraction Function Alpha
For 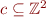 , define
, define
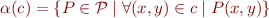
Example:
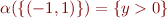
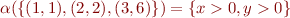
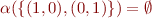
Monotonicity of Alpha
Let  .
.
We wish to prove that  .
.
Let 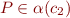 . Then for all
. Then for all 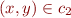 we have
we have 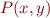 .
.
Then also for all 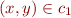 we have
we have 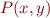 , because
, because  .
.
Therefore 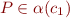 . We showed
. We showed  , so
, so  .
.
Alpha and Gamma are a Galois Connection
We show 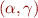 are a Galois Connection. We need to show that
are a Galois Connection. We need to show that

This is easy because both conditions reduce to
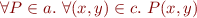
Not a Galois Insertion
Is it the case that 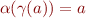 ?
?
We show this is not the case. This is because  is not injective.
is not injective.
Indeed, take 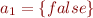 and
and 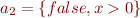 . Then
. Then
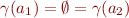
Note 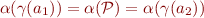 , but
, but 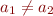 , but it is not the case
that
, but it is not the case
that 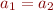 . In this particular case,
. In this particular case,
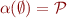
and  so
so
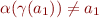
However, the approach works and is sound even without the condition 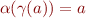 .
.
Least Upper Bound and Greatest Lower Bound
As expected, according to the syntactic ordering,  is
is  and
and  is
is  .
.
That means that, at control-flow graph join points, we intersect sets of predicates that are true on each of the incoming edges.
Computing sp sharp
Example:
Consider computing 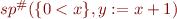 . We can test for each predicate
. We can test for each predicate  whether
whether
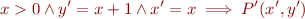
We obtain that the condition holds for  ,
,  , and for
, and for  , but not for
, but not for 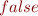 . Thus,
. Thus,
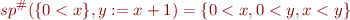
On the other hand,
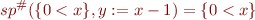
Fix some command given by relation  .
.
Denote 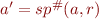 . We try to find how to compute
. We try to find how to compute  . As usual in Abstract Interpretation Recipe, for correctness we need to have
. As usual in Abstract Interpretation Recipe, for correctness we need to have
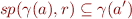
which, thanks to Galois connection is equivalent to
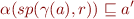
i.e.
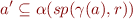
We wish to find the smallest lattice element, which is the largest set (this gives the tightest approximation). So we let
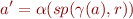
By observation above,
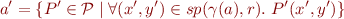
Let 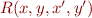 denote the meaning of relation
denote the meaning of relation  (according to e.g. Compositional VCG).
Then
(according to e.g. Compositional VCG).
Then 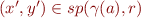 means
means
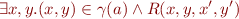
i.e.
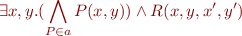
We then plug this expression back into  definition.
Because the existentials are left of implication, the result is:
definition.
Because the existentials are left of implication, the result is:
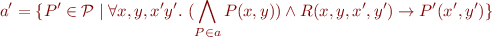
This is the rule to compute  .
.
In summary, to compute  , all we need to know is to check whether the following formula is valid
, all we need to know is to check whether the following formula is valid
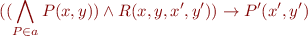
for given  and
and  .
.
Example of analysis run:
x = 0; y = 1; while (x < 1000) { x = x + 1; y = 2*x; y = y + 1; print(y); }
Take as the predicates  .
.
x = 0; y = 1; // 0<y, x<y,x=0,y=1, x<1000 // 0<y, 0<=x, x<y while (x < 1000) { // 0<y, 0<=x, x<y, x<1000 x = x + 1; // 0<y, 0<=x, 0<x y = 2*x; // 0<y, 0<=x, 0<x, x<y y = y + 1; // 0<y, 0<=x, 0<x, x<y print(y); } // 0<y, 0<=x, x<y, 1000 <= x
Pre-Computation using Weakest Preconditions
There is an alternative definition, which can be used to convert the above problem into a finite-state exploration problem. (It will be particularly useful if we consider an extension from conjunctions to disjunction of conjunctions.)
The condition
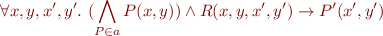
is equivalent to the validity of the formula
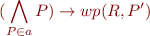
Fix a predicate 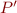 . Consider all
. Consider all  for which the above condition holds, define them as
for which the above condition holds, define them as
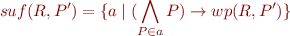
Clearly, if 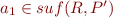 and
and 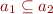 , then also
, then also 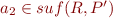 . So,
we can represent
. So,
we can represent 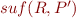 using its minimal elements
using its minimal elements 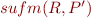 . These are minimal sufficient sets of predicates that ensure that
. These are minimal sufficient sets of predicates that ensure that
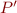 holds.
holds.
Then, we can define equivalently

The advantage of this definition is that we compute 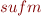 for a given predicate
for a given predicate 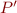 and command given by
and command given by 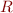 , and then we can efficiently compute
, and then we can efficiently compute  for all abstract values
for all abstract values  by checking inclusion of finite sets.
by checking inclusion of finite sets.
Approximation: The set 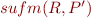 can have up to
can have up to 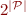 elements. To avoid this, we can restrict it to only those subsets
elements. To avoid this, we can restrict it to only those subsets  that have at most e.g. 3 predicates.
that have at most e.g. 3 predicates.
Note that using smaller 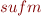 means that some
means that some  will be missing, the condition will be false in some cases, and in those cases
will be missing, the condition will be false in some cases, and in those cases 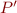 will not be included in the postcondition, so the resulting abstract element will be larger in the lattice. So the approach is still correct, just not as precise.
will not be included in the postcondition, so the resulting abstract element will be larger in the lattice. So the approach is still correct, just not as precise.
Further Techniques
Predicates per program point: Normally each program point has its own set of predicates. Indeed, these predicates may talk about local variables that only exist at those program points. The entire approach remains the same, just whenever computing the set of predicates at a program point  , use a local set
, use a local set 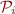 instead of one global set
instead of one global set 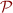 .
.
Further challanges:
- compute the sets
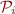 automatically, i.e. discover predicates automatically (usually through counterexample-guided abstraction refinement)
automatically, i.e. discover predicates automatically (usually through counterexample-guided abstraction refinement) - be more precise when handling paths through programs (path sensitivity, dependent attribute analysis)
- analyze procedures (context-free reachability)
See also predicate abstraction references.