Compositional Verification Condition Generator
Rules for Computing Formulas for Commands Compositionally
We compute for each command  the formula
the formula 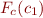 . We next show how to do it. These rules all follow from the semantics of our language.
. We next show how to do it. These rules all follow from the semantics of our language.
Assignment
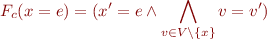
Assume
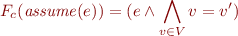
Havoc
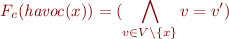
For simplicity of notation, in the sequel we work with state that has only one variable, x.
Union
Note
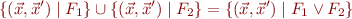
Therefore,
![Equation \begin{equation*}
F_c(c_1 [] c_2) = F_c(c_1) \lor F_c(c_2)
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img269b1545ef2e795d10a6f4fb2b738928.png)
Sequential Composition
Note that
![Equation \begin{equation*}
\begin{array}{l}
\{(\vec x,\vec x') \mid F_1 \} \circ \{(\vec x,\vec x') \mid F_2 \} \\
\qquad
= \{ (\vec x,\vec z) \mid F_1[\vec x':=\vec z] \} \circ \{ (\vec z,x') \mid F_2[\vec x:=\vec z] \} \\
\qquad
= \{ (\vec x,\vec z) \mid \exists \vec z. F_1[\vec x':=\vec z] \land F_2[\vec x:=\vec z] \}
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img15e344e6a5e8b99b6b1a94c4ef9f47ce.png)
Therefore,
![Equation \begin{equation*}
F_c(c_1\ ;\ c_2)\ =\ (\exists \vec z. F_c(c_1)[\vec x':=\vec z] \land F_c(c_2)[\vec x:=\vec z])
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imga41547545cb90cdc5ec4b8af8da159c3.png)
Above, ![Math $F_c(c_1)[\vec x':=\vec z]$](/w/lib/exe/fetch.php?media=wiki:latex:/img028c2cb5e5865679e5159103b3b2b9cd.png) denotes taking formula
denotes taking formula 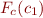 and replacing in it occurrences of variables
and replacing in it occurrences of variables  by variables
by variables  .
.
To avoid re-using variables, introduce always a fresh variable as  and denote it
and denote it  .
.
Loops?
The semantics for loops is given using transitive closure.
To express this, we would need a logic that supports transitive closure.
If we do this, our formulas will look very much like the programs and there are few good techniques for reasoning about them.
We will therefore deal with loops using alternative techniques (to be discussed later). A simple technique is unrolling loops.
Example
Take the program in the example below:
(if (x < 0) x=x+1 else x=x); (if (y < 0) y=y+x else y=y);
It translates into the following guarded command language:
![Equation \begin{equation*}
\begin{array}{l}
(assume(x<0) ; (x = x+1)\ [] assume (\lnot (x<0)) ; skip)\ ; \\
(assume(y<0) ; (y = y+x)\ [] assume(\lnot(y<0)) ; skip)
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgc9e95b3c88b8703aa5b6c9cc0fc1b40f.png)
Computing  for basic commands we obtain:
for basic commands we obtain:
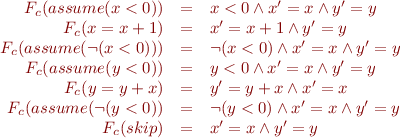
Applying innermost sequential compositions, we obtain
![Equation \begin{equation*}
\begin{array}{rcl}
F_c(assume(x < 0);x+x+1) &=&
\exists x_1,y_1.
\begin{array}[t]{l}
(x < 0 \land x'=x \land y'=y)[x':=x_1,y':=y_1] \land \\
(x' = x + 1 \land y' = y)[x:=x_1,y:=y_1] =
\end{array} \\
&=&
\exists x_1,y_1. x < 0 \land x_1 = x \land y_1 = y \land x'=x_1+1 \land y'=y_1 \\
& & \mbox{optional simplification step} \\
&=&
x < 0 \land x'=x+1 \land y'=y
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img7852e4a2e961104d8f441980af390c91.png)
We similarly obtain
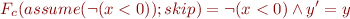
Thus, the meaning of the first if statement is:

We can similarly show that the meaning of the second 'if' statement is:
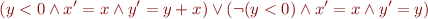
By applying renamings to  in first formula and
in first formula and 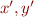 in the second formula, we obtain:
in the second formula, we obtain:
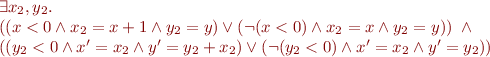
Note that, even if we had left the existential quantifiers over 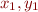 inside, we would be able to lift them to the top level through
inside, we would be able to lift them to the top level through  .
.
Useful Consequences of Rules
If  is a formula containing only unprimed variables, let
is a formula containing only unprimed variables, let 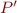 denote the formula where all program variables become primed (
denote the formula where all program variables become primed ( is replaced by
is replaced by 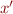 ).
More precisely
).
More precisely
![Equation \begin{equation*}
P' = P[x_1 := x'_1, \ldots, x_n := x'_n]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img349554eaba5bb23796bc71124792ba2c.png)
We then have the following:
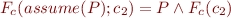
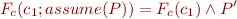
Formula Simplification: One-Point Rule
Assignments and assume statements generate equalities, many of which can be eliminated by one-point rule
![Equation \begin{equation*}
(\exists x. x=t \land F) \leftrightarrow F[x:=t]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgf56074f55fe9f416e0f42aa91741de9a.png)
There are more complex quantifier elimination procedures that can be used in principle as well.
Shape of Generated Formulas
Theorem: Consider a loop-free program  . Then each formula generated using the rules above is equivalent to
. Then each formula generated using the rules above is equivalent to

where 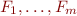 are formulas corresponding to havoc,assume (and assignment) statements (with some variables renamed), and
are formulas corresponding to havoc,assume (and assignment) statements (with some variables renamed), and  denotes a propositional combination that uses only
denotes a propositional combination that uses only  , and where the free variable in the above formula are unprimed and primed program variables. The resulting formula is polynomial in the size of
, and where the free variable in the above formula are unprimed and primed program variables. The resulting formula is polynomial in the size of  .
.
Proof: By induction on the structure of  . The base cases is trivial, taking
. The base cases is trivial, taking  to be the formula defining the relation. For the case of non-deterministic choice the property follows easily by lifting existential quantifiers to the top level and taking disjunction of the combinations
to be the formula defining the relation. For the case of non-deterministic choice the property follows easily by lifting existential quantifiers to the top level and taking disjunction of the combinations  . Similarly for sequential composition, where we do variable renaming and take conjunction of the combinations
. Similarly for sequential composition, where we do variable renaming and take conjunction of the combinations  .
.
To see that the 'compositional approach' generates a formula polynomial in the size of the program. Fix the set of variables  . Then:
. Then:
- the size of formula for each basic command is constant
- non-deterministic choice is disjunction
- sequential composition is conjunction (along with renaming that does not affect size)
Moreover, formula generated in such a way looks very much like the program itself, converted to static single assignment form, see
Using Computed Formulas to Obtain Verification Conditions
Suppose we wish to prove
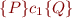
The resulting formula has the form:

which is equivalent to
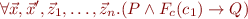
If we generate fresh variables for intermediate points, it suffices to prove the validity of the quantifier free formula:
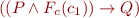
Equivalently, we need to prove unsatisfiability of the formula
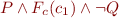
Further reading
- Semantics-based Program Analysis via Symbolic Composition of Transfer Relations, PhD dissertation by Christopher Colby, 1996