Exercises 05
We call relation 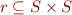 functional if
functional if 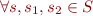 , if
, if 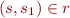 and
and 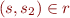 then
then 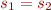 . For each of the following statements either give a counterexample or prove it:
. For each of the following statements either give a counterexample or prove it:
- if
 is functional,
is functional, 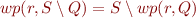
- if
 is functional,
is functional, 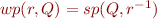
- for any
 ,
, 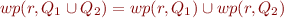
- if
 is functional,
is functional, 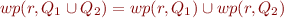
Rules for guarded commands
see sav07_homework_4 and its solution
Using the previously defined wp and  as the set of good states, define the relation
as the set of good states, define the relation  on commands by
on commands by

Note that this means that if we prove  correct, then
correct, then  is correct as well.
is correct as well.
3. Is  a partial order? Prove or give a counterexample.
a partial order? Prove or give a counterexample.
Define  as
as  .
.
4. Show
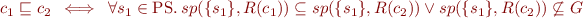
In other words,  holds iff for every execution of
holds iff for every execution of  from a state
from a state 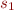 there is either the same execution in
there is either the same execution in  , or
, or  can produce an error.
can produce an error.
5. Define command skip as assert(True). Prove


![Math $c_1 \sqsubseteq c_2\ \rightarrow\ c_1 [] c_3 \sqsubseteq c_2 [] c_3$](/w/lib/exe/fetch.php?media=wiki:latex:/imgb2b9307f5bf39c544373630f69622484.png)
assume(F)  skip
skip  assert(F)
assert(F)
assert(F); assume(F)  assert(F)
assert(F)
assume(F); assert(F)  assume(F)
assume(F)
6. Prove the following shunting rules:

7. Let P be a guarded language program containing a statement c1. Suppose that
assume(pre); c1; assert(post)  havoc(x)
havoc(x)
Then show that if c2 is given by
assert(pre); havoc(x); assume(post)
then
P  P[c1:=c2]
P[c1:=c2]
where P[c1:=c2] denotes the result of substuting c2 instead of c1.