Syntax and Shorthands of HOL
We define HOL by introducing certain constants into Simply Typed Lambda Calculus and giving appropriate interpretations to them (through axioms or through semantics).
Types
We consider two base types:
- the type 'i' of 'i'ndividuals
- the type 'o' of truth values (the shorthand whose meaning to me is not 'o'bvious)
All types are built from i and o using function type constructor  . For example,
. For example,
- binary functions are terms of type
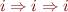 (arrow associates to the right, we use currying to represent functions with multiple arguments)
(arrow associates to the right, we use currying to represent functions with multiple arguments) - binary predicates are terms of type
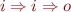
Logical Constants
To obtain a logic based on such lambda calculus, we add two family of constants:
- equality
 for each type
for each type  , denoting equality on elements of type
, denoting equality on elements of type 
- selection operator
 , denoting 'choice function' that takes a predicate and returns one element satisfying the predicate (if exactly one such element exists)
, denoting 'choice function' that takes a predicate and returns one element satisfying the predicate (if exactly one such element exists)
Everything else (most of mathematics) can be defined in this logic, and to a large extent has been done in systems such as Isabelle and HOL.
Defining Logical Functions
Of course, some of the following defined notions could have been taken as primitive, but this shows that they can also be considered as shorthands if we wish to keep the basic system simple. The definitions illustrate the expressive power of equality over functions:
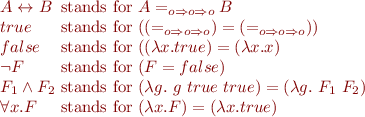
Note that we have defined negation, conjunction, and universal quantification, so all propositional operations and existential quantification are expressible.
We can also treat  ,
,  as operators, with the understanding that
as operators, with the understanding that  means
means 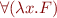 . In that case, the meaning of
. In that case, the meaning of  is:
is:
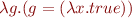
so that 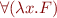 evaluates to
evaluates to 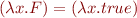 .
.
Note also that we can express
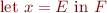
by 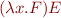 .
.
The selection operator  is not essential, but is a useful notation. By writing
is not essential, but is a useful notation. By writing
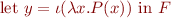
we can express the phrase “let y in F denote the unique x such that P(x) holds”.