Summary Example with Integers
var a = new Array[Int](2*N) var i = 0 while // loop invariant: 0 <= i && i <= N (i < N) { a[2*i] = 0 a[2*i+1] = 1 i = i + 1 }
We can show that the invariant is preserved and that the invariant implies that there are no array out of bounds errors.
Verification condition that there is no array our of bound error:

The negation of the condition:
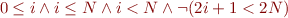
This condition is clearly unsatisfiable. One way to prove this is to use quantifier elimination. Because the condition has no quantifiers, there are additional methods.
Today:
- mention some additional methods
- introduce the idea of small-model theorems
- give a notion of handling non-numerical constraints