Proof Rules for Equality
Paramodulation
![Equation \begin{equation*}
\frac{D \cup \{ s = t \}\ \ \ \ C[s'] }
{subst(\sigma)(D \cup C[t])}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img974b4b33c3d33c3b12269382b51b5928.png)
where  is mgu of
is mgu of 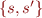 .
.
Here ![Math $C[s']$](/w/lib/exe/fetch.php?media=wiki:latex:/imgab264042a9924e39dd547d53585371a7.png) means that
means that 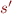 occurs somewhere in
occurs somewhere in  ; then
; then ![Math $C[t]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgc64a70df093ce0bf31fd8273fe291962.png) results from replacing that occurrence of
results from replacing that occurrence of 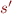 with
with  .
.
Equality Resolution
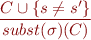
where  is mgu of
is mgu of 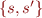 .
.
Superposition: a closely related technique to paramodulation, also meant for dealing with equality.