Interval Analysis and Widening
Interval analysis domain, for each program point, maps each program variable to an interval.
Interval bounds may be  and
and  . Interval
. Interval ![Math $[-\infty,+\infty]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgb4adf0b8ef783638901d0ebe43bbf68c.png) represents no constraints.
represents no constraints.
Analysis domain has elements  where
where  denotes the set of such intervals.
denotes the set of such intervals.
How to interpret a command

for some operation  ?
?
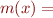
What does the lattice of intervals look like?
Height of lattice of one interval for 64-bit integers:
If we have  variables in program and
variables in program and  program points, height of lattice for the analysis domain is
program points, height of lattice for the analysis domain is  times larger.
times larger.
For unbounded integers, lattice is unbounded.
How to guarantee termination?
Widening technique: if we do not seem to be converging, make a “jump”.
Finite set of “jump points”  (e.g. set of all integer constants in the program)
(e.g. set of all integer constants in the program)
In fixpoint computation, compose  with function
with function
![Equation \begin{equation*}
w([a,b]) = [\max \{x \in J \mid x \le a\},
\min \{x \in J \mid b \le x\}]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img6af571558de83b412691681a24c9419d.png)
Approaches:
- always apply widening (we will assume this)
- iterate a few times with
 only (without using
only (without using  ), if not a fixpoint at this program point, then widen.
), if not a fixpoint at this program point, then widen.- this is not monotonic: if you start at fixpoint, it converges, if start below, can jump over fixpoint
Standard iteration: 
Widening: 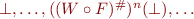
Here,  for all
for all  by definition of
by definition of 
Narrowing: after finding fixpoint of 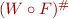 , apply
, apply  to improve precision.
to improve precision.
Observation: if  and
and  are
are  -continuous functions and
-continuous functions and  for all
for all  , then narrowing will improve the result, that is, if
, then narrowing will improve the result, that is, if 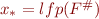 and
and 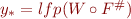 , then
, then  and
and
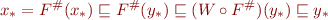
![Equation \begin{equation*}
[\min \{v_y \otimes v_z \mid v_y \in m(y), v_z \in m(z) \},
\max \{v_y \otimes v_z \mid v_y \in m(y), v_z \in m(z) \}]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgec9cf67f7ee98b5de353f1415844fc21.png)
