Homework 05 - due 2 April 2008 (after break)
Problem 1
Extend the DPLL SAT solver from homework04 with the ability to generate resolution proofs.
As before, if a given formula is satisfiable, the SAT solver should produce an assignment to all variables such that the formula evaluates to true under this assignment.
Additionally, if a given formula is unsatisfiable, the SAT solver should produce unsatisfiability proof in some format. Use proof trees for resolution proofs, whose nodes indicate the variable on which resolution is performed and contain subtrees for proofs of clauses on which resolution is performed.
- you can also use Tracecheck format for TraceCheck tool from BooleForce solver
Optional extension (can be used for project): Extend this solver with 2-literal watching, lemma learning and heuristics. You can look at the source code of existing implementations to gain insight into techniques (such as http://sourceforge.net/projects/dpt ) but you are not allowed to copy it, you must write your own implementation.
We will run a small competition of implemented solvers.
Note that it can be useful to know about SAT solvers.
Test examples shown in the class:
Problem 2
Consider the notion of Substitutions for First-Order Logic.
Part a) Consider an implementation of that definition of sfsubst as a recursive function on syntax trees that directly follows its definition. Consider formulas with many identical quantifiers, 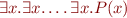 . More precisely, let
. More precisely, let 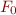 denote formula
denote formula 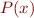 and
and  denote formula
denote formula 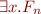 for all
for all  . How many accesses to syntax tree nodes does this function perform on the abstract syntax tree of formula
. How many accesses to syntax tree nodes does this function perform on the abstract syntax tree of formula  ?
?
Part b) Define the “fast, safe” substitution, fsfsubst, with the property that for a formula with  syntax tree nodes, the number of accesses to syntax tree nodes is
syntax tree nodes, the number of accesses to syntax tree nodes is 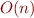 . (You do not need to implement it, but this may be helpful if for you to debug your definition.)
. (You do not need to implement it, but this may be helpful if for you to debug your definition.)
Part c) Prove (using appropriate proof technique) that your definition of fsfsubst has the property
![Equation \begin{equation*}
e_F(fsfsubst(\{x_1 \mapsto t_1,\ldots,x_n \mapsto t_n\})(F))(I) = e_F(F)(I[x_1 \mapsto e_T(t_1)(I),\ldots, x_n \mapsto e_T(t_n)(I)])
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgd2a1fabc9f7b338569a649a99c6b4a2f.png)
You can assume that formulas are built using only these symbols:
- one constant

- one unary function symbol

- one binary relation symbol
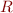
- operations
 ,
,  ,
,  as the only logical operations.
as the only logical operations.
Problem 3
Consider the definition of Consequence set defined in First-Order Logic Semantics.
Prove that it satisfies these properties where  ,
,  denote sets of formulas.
denote sets of formulas.
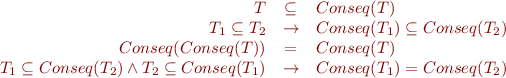
Problem 4 (Optional)
Use Compactness for First-Order Logic to prove the following theorem:
If a set  of sentences has arbitrarily large finite models (that is, for every
of sentences has arbitrarily large finite models (that is, for every  , there exists a model
, there exists a model 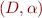 with
with  a finite set of at least
a finite set of at least  elements), then
elements), then  has an infinite model.
has an infinite model.