Build a verification condition generator based on forward symbolic execution, extending Problem 4 from homework02 and using the description of Forward Symbolic Execution from lecture05.

You do not need to parse program text, you can simply generate test cases by writing syntax trees.

Your verification condition generator should work in the presence of loops, assuming that the program is annotated with loop invariants expressed as 'assert' statements written before the loop.

Connect your program to a theorem prover to prove the verification conditions. You can

• feed them into the formDecider.opt prover from the Jahob system or
• use SMT-LIB format and a prover such as CVC3

Prove correctness of polarity-based improvements for satisfyability-preserving transforming to CNF.

Prove that there is no polynomial-time algorithm for transforming a propositional formula into an equivalent formula in conjunctive normal form. You do not need to use any deep results of complexity theory.

Specifically, prove that there exists an infinite family of formulas 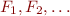such that for each , every algorithm that transforms to CNF needs exponential time. (Note that it is not enough to prove that one particular algorithm will take exponential time, you need to prove that every algorithm would need exponential time.)

Extend propositional formulas with NAND operator, denoted and defined by \[

  x \barwedge y = \lnot (x \land y)

\] Show that for each propositional formula there exists an equivalent formula that uses as the only operator.