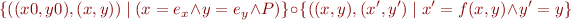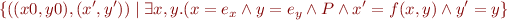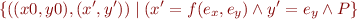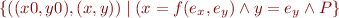Forward Symbolic Execution
Can be used for
- verification condition generation
- executing programs
- testing, bug finding
- proving programs correct (if extended with techniques for loop invariants)
Basic Ideas
Generalize an interpreter to work with symbolic instead of concrete values.
Assume the set of variables 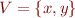 .
.
Symbolic execution maintains a formula 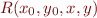 describing the relation between the initial state and the current state.
describing the relation between the initial state and the current state.
Exploiting Analogy with Execution
Maintain symbolic state formula 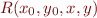 in the following normal form:
in the following normal form:
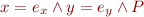
where  is term describing symbolic state of
is term describing symbolic state of  and
and 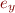 describes symbolic state of
describes symbolic state of  . The remaining part of the formula
. The remaining part of the formula  is given in path condition
is given in path condition  . It is a conjunction of all branch conditions up to current program point. We require
. It is a conjunction of all branch conditions up to current program point. We require  to be expressed only in terms of
to be expressed only in terms of 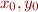 , not
, not  .
.
Checking Assertions
Postcondition at current program point is 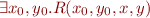 .
.
Branch Pruning
If condition  ever becomes contradictory, relation is empty and symbolic execution can stop (path is unreachable).
ever becomes contradictory, relation is empty and symbolic execution can stop (path is unreachable).
Special case: if initial condition specifies values of variables, then we know which branch to enter.
Symbolic Execution Rules
We derive these rules from semantics, taking into account the definition of R in terms of e_x,e_y,P.
Assignment
Assume
Given
assume(F)
change state:
P := P & F[x<-e_x, y<-e_y]
Havoc
Given
havoc(x)
change state:
e_x := x_k
where x_k is a fresh variable.
Assert
Given
assert(F(x,y))
emit proof obligation:
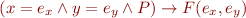
and change the state:
x := x_k (fresh) y := y_k (fresh) P := F
Sequential composition
Handled implicitly: execute statements one by one.
Non-deterministic choice
Execute both branches and collect proof obligations from both branches.
Exponential explosion remedy:
- work on control-flow graph
- merge symbolic states when edges merge
Merging: Given two symbolic states:
x = e_x1 & y = e_y1 & P1 x = e_x2 & y = e_y2 & P2
generate a single symbolic state
x = x_k & y = y_k & P
where P is ((x_k = e_x1 & y_k = e_y1 & P1) | ((x_k = e_x2 & y_k = e_y2 & P2)
Then we continue only from this one state.
Execution
If the first statements are
assume (x=0) assume (x=1)
Then symbolic execution knows the exact values and can work as an interpreter.
Underapproximations
Here we generate real counterexamples (underapproximation), we compute smaller relation than one given by program semantics.
If there are no loop invariants, we can still execute program on concrete inputs. For symbolic initial state (e.g. giving upper bound of loop) execution need not terminate.
- Bounding depth: stop executing for paths longer than some value
- Bounding state: small integer width, small number of objects in heap
- Loop unrolling: replace loop( c ) with c[]c;c[]c;c;c for some number of times
- Instantiating values: find a satisfying assignment for R, take value v of x in it and replace e_x with v (moves towards concrete execution)
Overaproximation
In this case we compute overaproximation, bigger relation than the actual relation given by program semantics.
Examples:
- do not maintain exact expressions for variables, but only whether they are positive
- maintain only linear or certain polynomial constraints - if actual constraints are more complex, keep only the polynomial constraints that are guaranteed to hold
Why we approximate we can obtain
- termination even for programs that have loops
- useful information about the program (not exactly all information that we are interested in, depends on the approximation)
References
- Symbolic execution and program testing by James C. King (pdf)
- Lori Clarke and Debra Richardson: Symbolic Evaluation Methods for Program Analysis, in Program Flow Analysis: Theory and Applications, Prentice-Hall 1981.
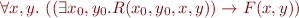
 .
.