Homework 03
Problem 1: NAND
Extend propositional formulas with NAND operator, denoted  and defined by
and defined by
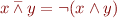
Show that for each propositional formula  there exists an equivalent formula that uses
there exists an equivalent formula that uses  as the only operator.
as the only operator.
Problem 2: Satisfiability-Preserving Transformation to CNF
Your goal here is to prove key steps in transformation of a formula containing  to equisatisfiable CNF formula. The key transformation steps that introduce fresh variables for formula subtrees can be summarized as follows:
to equisatisfiable CNF formula. The key transformation steps that introduce fresh variables for formula subtrees can be summarized as follows:
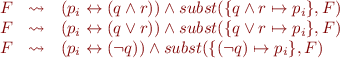
Note that each introduced equivalence, such as, 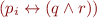 can generate several clauses. Suppose now that
can generate several clauses. Suppose now that  is in negation-normal form. Show that we can replace some of these equivalences with implications. Write the new transformation rules and prove that they produce equisatisfiable formulas.
is in negation-normal form. Show that we can replace some of these equivalences with implications. Write the new transformation rules and prove that they produce equisatisfiable formulas.
Problem 3: Equivalence Preserving Transformation to CNF
Prove that there is no polynomial-time algorithm for transforming a propositional formula into an equivalent formula in conjunctive normal form. You do not need to use any deep results of complexity theory.
Specifically, prove that there exists an infinite family of formulas 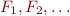 such that for each
such that for each  , every algorithm that transforms
, every algorithm that transforms  to CNF needs exponential time. (Note that it is not enough to prove that one particular algorithm will take exponential time, you need to prove that every algorithm would need exponential time.)
to CNF needs exponential time. (Note that it is not enough to prove that one particular algorithm will take exponential time, you need to prove that every algorithm would need exponential time.)
Problem 4: Verification Condition Generator using Symbolic Execution
Build a verification condition generator based on forward symbolic execution, extending Problem 4 from homework02 and using the description of Forward Symbolic Execution from lecture05.
You do not need to parse program text, you can simply generate test cases by writing syntax trees.
Your verification condition generator should work in the presence of loops, assuming that the program is annotated with loop invariants expressed as 'assert' statements written before the loop.
Connect your program to a theorem prover to prove the verification conditions. You can
- feed them into the formDecider.opt prover from the Jahob system or
- use SMT-LIB format and a prover such as CVC3