Homework 02
Deadlines:
- Problem 1 and Problem 2 are due 5 March 2008 at 11:00am
- Problem 3 and Problem 4 are due 6 March 2008 at 08:00am
Problem 1
Using definitions of Hoare triple, sp, wp in Hoare logic, prove the following:
- the law on the postcondition of inverse versus wp
- the equivalence of the Three Forms of Hoare Triple.
Problem 2
We call relation 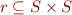 functional if
functional if 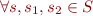 , if
, if 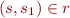 and
and 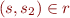 then
then 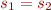 . For each of the following statements either give a counterexample or prove it:
. For each of the following statements either give a counterexample or prove it:
- for any
 ,
, 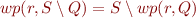
- if
 is functional,
is functional, 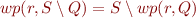
- for any
 ,
, 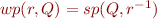
- if
 is functional,
is functional, 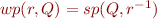
- for any
 ,
, 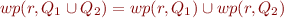
- if
 is functional,
is functional, 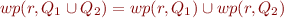
Problem 3
Write an interpreter for our simple programming language with the additional ability to state assume statements, assert statements, and loop invariants. The meaning of assignments and control structures is the same as in the usual programming language. For assume and assert statements, the interpreter should just check whether they are true in the current program state and emit a warning if they are not.
Use Scala integers to represent the unbounded integers in the language.
Your interpreter should take an abstract syntax tree of the program and keep executing the program until it terminates (if it does not terminate, the interpreter should also not terminate). If the program terminates, your interpreter should print the final state of the program.
Here is an example abstract syntax tree that you may wish to use. There is no need to write a parser for this language, you can start from syntax trees.
sealed abstract class Term case class Constant(val c: Int) extends Term case class Variable(val v: String) extends Term case class Plus(val t1: Term, val t2: Term) extends Term case class Minus(val t1: Term, val t2: Term) extends Term case class Times(val c: Int, val t: Term) extends Term case class Divide(val t: Term, val c: Int) extends Term case class Modulo(val t: Term, val c: Int) extends Term sealed abstract class BoolExpr case class Equal(val t1: Term, val t2: Term) extends BoolExpr case class LessThan(val t1: Term, val t2: Term) extends BoolExpr case class GreaterThan(val t1: Term, val t2: Term) extends BoolExpr case class Negation(val F: BoolExpr) extends BoolExpr case class And(val f1: BoolExpr, val f2: BoolExpr) extends BoolExpr case class Or(val f1: BoolExpr, val f2: BoolExpr) extends BoolExpr sealed abstract class Command case class Assignment(val v: String, val t: Term) extends Command case class IfThenElse(val cond: BoolExpr, val ifcom: Command, val elsecom: Command) extends Command case class Block(val com1: Command, val com2: Command) extends Command case class WhileLoop( cond: BoolExpr, val com: Command) extends Command
Problem 4
Extend the previous interpreter with elements of symbolic execution. A symbolic execution engine computes the formula 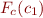 that represents the relation associated with the command
that represents the relation associated with the command  . It is similar to an interpreter but works with symbolic state containing two parts:
. It is similar to an interpreter but works with symbolic state containing two parts:
- mapping from each variable into an expression denoting its value as a function of the initial state, the initial state being denoted by symbolic variables.
- a constraint on the variables
For a program with variables x,y, the initial state of symbolic execution is a map with constraint true:
map: {"x"->Var("x0"), "y"->Var("y0")}
constraint: True
After executing assignment
x = x + y
the resulting symbolic state is
map: {"x"->Plus(Var("x0"),Var("y0")), "y"->Var("y0")}
constraint: True
If afterwards we execute
y = x + 1
the resulting symbolic state is
map: {"x"->Plus(Var("x0"),Var("y0")), "y"->Plus(Plus(Var("x0"),Var("y0")),Constant(1))}
constraint: True
If after this we execute a statement
assume (x > 0)
the resulting symbolic state is
map: {"x"->Plus(Var("x0"),Var("y0")), "y"->Plus(Plus(Var("x0"),Var("y0")),Constant(1))}
constraint: GreaterThan(Plus(Var("x0"),Var("y0")),Constant(0))
Write a program that executes a givn loop-free command (containing sequential composition “;”, if-then-else, assume, and assignments “:=”). The program should start from the initial symbolic state and prints the resulting final symbolic state. Given a command “c” with two variables x,y, if the final symbolic state is
map: {x->e1, y->e2}
constraint: F
then the relation representing the meaning of  should be given by the relation
should be given by the relation
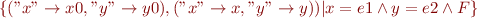
The final formula  may or may not use additional existentially quantified variables.
may or may not use additional existentially quantified variables.
Problem 5 (optional alternative to Problem 4)
(See also homework03.)
Extend the interpreter of Problem 3 with a verification-condition generator based on symbolic execution. Verification condition generator should produce verification conditions where 'assume' becomes an assumption and where 'assert' becomes an assertion to be checked. It should emit one verification condition for each 'assert'. It should also check that all loop invariants are preserved. To prove the verification conditions, your verification-condition generator can feed them into the formDecider.opt prover from the Jahob system.