Correctness of A/G Reasoning
Correctness as Approximation of Relations
Specification  provides a relation that is intended to approximate relation
provides a relation that is intended to approximate relation  defining the meaning of procedure, that is, we would like to prove
defining the meaning of procedure, that is, we would like to prove

Following Relational Semantics of Procedures, consider one procedure and its associated function
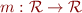
and its fixed point  .
.
The idea of approach based on specifications is to prove that, if we assume that procedure calls satisfy the specification, then we can prove the specification for the procedure we are verifying. In other words, specifications provide a relation  such that
such that
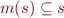
We claim that  where
where 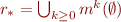 .
.
Proof:
Expressing Approximation Using Assume and Assert
Consider a program with only one state variable  .
.
We express our approximation as
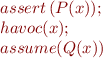
So, we would like to show that
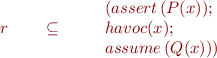
is implied by the condition we are checking:
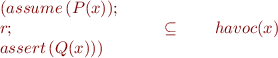
Shunting rules
Recall Assert and error conditions. We say that relation  respects errors if for an error state
respects errors if for an error state  we have
we have 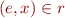 for all states
for all states  .
.
For relations  ,
,  that respect errors, we have
that respect errors, we have


Proofs:
- using relations
- using weakest preconditions (see homework in SAV'07)
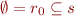 , and by monotonicity of
, and by monotonicity of  we obtain that
we obtain that  implies
implies 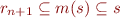 . Therefore,
. Therefore,  , so
, so  ) we can show by induction starting from innermost call. The innermost call has no recursive invocation, so it presents the base case of induction.
) we can show by induction starting from innermost call. The innermost call has no recursive invocation, so it presents the base case of induction.