Combining Decision Procedures
Merging Models of Theories with Disjoint Languages (Signatures)
Theorem: Let  be a finite language
be a finite language  where
where  . Let
. Let  be a conjunction in language
be a conjunction in language  , and for
, and for 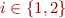 let
let  be those literals from
be those literals from  whose symbols appear only in
whose symbols appear only in  , as well as equality and disequality literals. Suppose further that if variables
, as well as equality and disequality literals. Suppose further that if variables 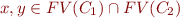 then either
then either  appears in
appears in  or
or 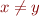 appears in
appears in  (thus they also appear in
(thus they also appear in  and
and  ). Let
). Let  be a set of sentences in language
be a set of sentences in language  for
for 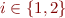 . Suppose there exists a model for
. Suppose there exists a model for  for
for 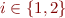 and that these models have domains of same cardinality. Then there exists a model for
and that these models have domains of same cardinality. Then there exists a model for  .
Note: for
.
Note: for  to satisfy the condition, it suffices for it to be flat and to contain equality or disequality for all common variables. One possible way to achieve this is Atomic Diagram Normal Form but there is no need to do case analysis on literals other than equality literals.
to satisfy the condition, it suffices for it to be flat and to contain equality or disequality for all common variables. One possible way to achieve this is Atomic Diagram Normal Form but there is no need to do case analysis on literals other than equality literals.
Proof (using merging of models): There exists an isomorphism of interpretation 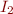 such that the resulting structure
such that the resulting structure 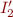 agrees with
agrees with 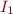 on the common variables. Extending
on the common variables. Extending 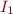 with interpratation of symbols in
with interpratation of symbols in 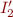 we obtain the desired model. End.
we obtain the desired model. End.
Proof (using interpolation): First-order logic has interpolation property, by Craig's interpolation theorem. Suppose we have models for
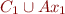 and
and 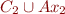 , but that there is no model for
, but that there is no model for
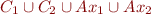 . By compactness for first-order logic there exists a finite subset that is contradictory. By interpolation there exists an interpolant
. By compactness for first-order logic there exists a finite subset that is contradictory. By interpolation there exists an interpolant  that is, say, implied by
that is, say, implied by 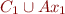 and contradictory with
and contradictory with 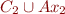 . The interpolant is in the common language, so it contains only equalities. It can be quantified, but over infinite domains quantifiers can be eliminated in a very simple way (and in any case, it is a fragment of BAPA that has QE). So, the result is a disjunction of conjunctions of equalities and disequalities among the common variables. But because
. The interpolant is in the common language, so it contains only equalities. It can be quantified, but over infinite domains quantifiers can be eliminated in a very simple way (and in any case, it is a fragment of BAPA that has QE). So, the result is a disjunction of conjunctions of equalities and disequalities among the common variables. But because  and
and  contain a complete atomic type, they either imply or are contradictory with
contain a complete atomic type, they either imply or are contradictory with  , depending on whether the atomic diagram normal form contains the atomic type present in
, depending on whether the atomic diagram normal form contains the atomic type present in 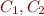 or not. Note that
or not. Note that  is contradictory since
is contradictory since  is interpolant, so each conjunct in its DNF is contradictory. Therefore,
is interpolant, so each conjunct in its DNF is contradictory. Therefore,  does not have as a disjunct the atomic diagram present in
does not have as a disjunct the atomic diagram present in  or
or  . Then
. Then  is contradictory with
is contradictory with  as well. Since
as well. Since  is a consequence of
is a consequence of 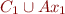 , it follows that
, it follows that 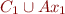 is contradictory. But we assumed it is satisfiable. End
is contradictory. But we assumed it is satisfiable. End
Example: Take formula
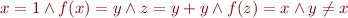
If we take a finite model for uninterpreted functions, we cannot merge it with the model for addition. But there is an infinite model for uninterpreted functions as well, and we can merge this model with the model for integers.
Stable Infiniteness
We wish to use different decision procedures to check  satisfiability.
satisfiability.
How do we know whether models have same cardinality?
- decision procedure could tell us cardinality of model which it found (see Combined Satisfiability Modulo Parametric Theories)
- we only work with theories that are guaranteed to have infinite models - stable infiniteness requirement
Definition: Theory  is stably infinite iff for every quantifier-free formula
is stably infinite iff for every quantifier-free formula  , if
, if 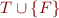 is satisfiable then
is satisfiable then 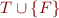 has an infinite model.
has an infinite model.
In practice this is not a restriction.
One way to ensure this: make sure that  only has infinite models by adding axioms that there exists at least
only has infinite models by adding axioms that there exists at least  elements for all
elements for all  .
.
- if we need to reason about some number of finitely many elements, add a unary predicate and look at elements that satisfy it
Example: The following theories are stably infinite:
- integers, rationals (in fact, they have only infinite models, because they can define irreflexive total order)
- uninterpreted function symbols: add fresh elements (they do not participate in satisfying assignment of quantifier-free formula)
Combining Decision Procedures By Guessing Arrangements
Suppose we have a collection of decision procedures for stably infinite theories.
Algorithm for deciding quantifier-free formulas in union of those theories:
- generate a conjunction (using SAT solver)
- flatten conjunction and separate it into different theories
- guess an arrangement of equalities (this is additional case analysis)
- apply decision procedure with its literals and the guessed arrangement
This method is complete for quantifier-free formulas:
- if a decision procedure says UNSAT, the conjunction is UNSAT (because conjunctions given to theories are weaker than the entire conjunction)
- if all conjuncts are UNSAT (for all arrangements, for all SAT disjuncts), the problem is UNSAT
- if some conjunct, for some arrangement, is SAT for all decision procedures, then the Theorem above says that the entire conjunction is SAT, so problem is SAT
Convex Theories
Convex theories are theories that allow us to avoid guessing the arrangement.
Idea: instead of just checking SAT/UNSAT, the decision procedure will derive all equalities that follow from the conjunction.
In some cases there is no single equality that follows, but only a disjunction can be derived:
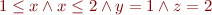
implies  but not any other non-trivial equality between variables. We say integer linear arithmetic is a non-convex theory.
but not any other non-trivial equality between variables. We say integer linear arithmetic is a non-convex theory.
Definition: Theory  is convex iff for every conjunction of literals
is convex iff for every conjunction of literals  , the condition
, the condition 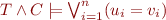 implies that there exists
implies that there exists  such that
such that
 .
.
In short, a formula in convex theory implies a disjunction iff it implies one of the disjuncts.
Examples of convex theories
- linear arithmetic over rational numbers
- quantifier-free uninterpreted functions
- quantifier-free term algebras
Equality Propagation
Instead of guessing arrangement, split the literals and let theories derive equalities and disjunctions of equalities, and propagate it to all other theories.
- convex theories propagate only individual equalities
- non-convex theories propagate disjunctions of equalities
This is the Nelson-Oppen technique for combining decision procedures.
To see completeness, consider the stage when no theory has new equalities or disjunctsions of equalities to report. Take the conjunction of negations of all remaining atomic formulas. We claim that this is satisfiable for all theories. Indeed, if it was not, then the negation of this conjunction would be implied by one of the theories.
Theory Propagation
Why derive only new equalities and rely on SAT solver to guess literals?
- if theory concludes that a literal must be true, it selects it
- can improve efficiency if the algorithm for theory anyway derives such information
Recent approach - try to propagate candidate equalities (even if they are not implied)
- Model-based Theory Combination, Leonardo de Moura and Nikolaj Bjørner, Workshop on Satisfiability Modulo Theories (SMT), Berlin, Germany, 2007.
Complexity
- if each theory is convex and polynomial time (e.g. congruence closure + real linear arithmetic), then conjunctions can be decided in PTIME
- if each theory is NP (e.g. we also allow integer linear programming), then (even for non-convex theories), any quantifier-free combination is in NP
Theories with Non-Disjoint Languages
Essentially, what is shared between conjunctions of literals in languages in  and
and  is the equality symbol. If more than equality is shared, then interpolation theorem tells us that we may need to exchange quantified formulas. If we have quantifier elimination for the theory of shared signature, then it suffices to exchange quantifier-free formulas.
is the equality symbol. If more than equality is shared, then interpolation theorem tells us that we may need to exchange quantified formulas. If we have quantifier elimination for the theory of shared signature, then it suffices to exchange quantifier-free formulas.
The correctness proof for Nelson-Oppen techniques in Calculus of Computation Textbook, Section 10.4 uses a proof of Theorem stated above that would generalize to the case of some other theories that admit quantifier elimination.
Proof idea:
- FOL has interpolation property
- if the formula is unsatisfiable, there exists an interpolant in language
 , which generalizes the notion of arrangement for equalities
, which generalizes the notion of arrangement for equalities - if we have quantifier elimination for formulas in
 with respect to
with respect to  , then arrangements are quantifier-free
, then arrangements are quantifier-free
Alternative method: