Atomic Diagram Normal Form
We next consider a syntactic normal form that helps us understand the decidability of the combination problem.
Flat Form
By introducing fresh variables, each conjunction of literals can be represented as an equisatisfiable conjunction of only “flat literals”, which are flat atomic formulas or their negation, where flat atomic formula is


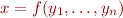
We call this “flat form” of the conjunction of literals. (We can also eliminate 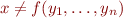 if needed.)
if needed.)
Rewrite rule that describes this transformation:
![Equation \begin{equation*}
C[t] \ \ \leadsto \ \ (x=t) \land C[x]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imge4531d8837d1d854a0d747f82d85826e.png)
Example: Represent  as
as
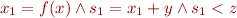
Finiteness of Flat Literals with Fixed Variables
Consider a formula in flat form. Let language  contain only the symbols occurring in the formula. For the fixed set of variables occurring there is a finite number of flat atomic formulas.
contain only the symbols occurring in the formula. For the fixed set of variables occurring there is a finite number of flat atomic formulas.
Assume  variables. (
variables. ( )
)
Number of 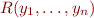 is:
is: 
Number of  atomic formulas is:
atomic formulas is: 
Number of 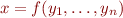 literals is:
literals is: 
Note: if we did not have only flat literals, we could have infinitely many atomic formulas, because of arbitrarily large terms.
Example: When we have relation symbols  and no function symbols, and consider 3 variables
and no function symbols, and consider 3 variables  ,
, ,
, , possible atomic formulas are:
, possible atomic formulas are:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
and there are 3^2+3^2=18 atomic formulas.
Atomic Diagram Normal Form
For each flat literal  ,
,  is equivalent to
is equivalent to 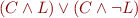 and
and  is a conjunction of flat literals.
is a conjunction of flat literals.
Let variables of  be
be  .
.
Atomic diagram conjunction is a flat form such that for each flat atomic formula  in variables
in variables  either
either  or
or 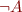 appears.
appears.
Each conjunction of flat literals is equivalent to a disjunction of atomic diagram conjunctions. Such form can be very large and we do not need to go that far, but we can when we need to.
Note: if we simply guess all possible conjunctions of literals and negations, some of them will be unsatisfiable in the theory. Those are useless and we should eliminate them. For example, if we consider equality literals, then
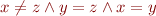
is unsatisfiable. Only those conjunctions of equality literals can be satisfiable that correspond to an equivalence relations on variables. Such conjunction of literals that corresponds to an equivalence relation is called arrangement in the context of combination techniques.
 can be rewritten as such (notating
can be rewritten as such (notating 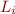 the
the 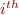 flat literal and
flat literal and  the truth value of the
the truth value of the 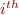 variable):
variable):
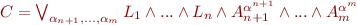
Which in turn can be rewritten as (notating  the
the 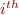 possible arrangement):
possible arrangement):
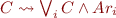
Example: In last example, there are 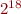 disjuncts to consider. If relations have special properties many cases are unsatisfiable and can be ignored. Nevertheless, the number of satisfiable atomic diagram formulas is typically exponential.
disjuncts to consider. If relations have special properties many cases are unsatisfiable and can be ignored. Nevertheless, the number of satisfiable atomic diagram formulas is typically exponential.
For example, if we have only equality symbol, each partition of the set of variables gives one satisfiable formula (asserting that elements in same partition are equal, in different partitions disequal). Partition 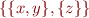 gives formula
gives formula
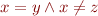
or, if we include all atomic formulas:

The number of partitions is given by Bell numbers.