LARA – Lab for Automated Reasoning and Analysis -

"Dreadbury Mansion Mystery” example

Exercise: Encode the following text in English into First-order logic:

Someone who lives in Dreadbury Mansion killed Aunt Agatha. Agatha, the butler, and Charles live in Dreadbury Mansion, and are the only people who live therein. A killer always hates his victim, and is never richer than his victim. Charles hates no one that Aunt Agatha hates. Agatha hates everyone except the butler. The butler hates everyone not richer than Aunt Agatha. The butler hates everyone Aunt Agatha hates. No one hates everyone. Agatha is not the butler.

Solution:

Let 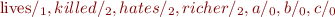$lives/_1, killed/_2, hates/_2, richer/_2, a/_0, b/_0, c/_0$ be a first-order signature. Then the above text can be formalized as follows:

$\exists x. lives(x) \land killed(x,a)$

$lives(a) \land lives(b) \land lives(c) \land \forall x. lives(x) \rightarrow (x=a \lor x=b \lor x=c)$

$\forall x. \forall y. killed(x,y) \rightarrow (hates(x,y) \land \neg richer(x,y))$

$\forall x. hates(a,x) \rightarrow \neg hates(c,x)$

$\forall x. hates(a,x) \leftrightarrow x \not\approx b$

$\forall x. \neg richer(x,a) \leftrightarrow hates(b,x)$

$\forall x. hates(a,x) \rightarrow hates(b,x)$

$\neg \exists x. \forall y. hates(x,y)$

$a \not\approx b$

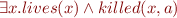
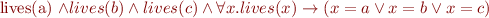
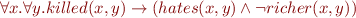
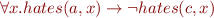
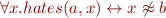
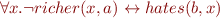
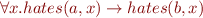
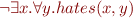
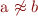
Those formulas are represented as the input language of various tools (SPASS, Jahob system, Isabelle/HOL) in Tools demo

Further references

Attempto controlled English