LARA

Normal form for loop-free programs

Example: 

(if (x < 0) x=x+1 else x=x);
(if (y < 0) y=y+x else y=y);

Without loops, after expressing conditionals using [] we obtain 

c ::=  x=T | assume(F) |  c [] c  |  c ; c

Laws:

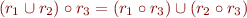
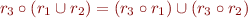
\begin{equation*} (r_1 \cup r_2) \circ r_3 = (r_1 \circ r_3) \cup (r_2 \circ r_3) \end{equation*}

\begin{equation*} r_3 \circ (r_1 \cup r_2) = (r_3 \circ r_1) \cup (r_3 \circ r_2) \end{equation*}

Normal form:

\begin{equation*} \bigcup_{i=1}^n p_i \end{equation*}

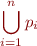
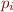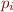Each $p_i$ is of form $b_1 \circ \ldots \circ b_k$ for some $k$, where each $b_i$ is assignment or assume. Each $p_i$ corresponds to one of the finitely paths from beginning to end of the acyclic control-flow graph for loop-free program.

Length of normal form with sequences of if-then-else.

We want to show:

\begin{equation*} \{ P \} r \{ Q \} \end{equation*}

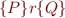
Verifying Each Path Separately

By normal form this is

\begin{equation*} \{ P \} \bigcup_{i=1}^n p_i \{ Q \} \end{equation*}

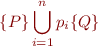
which is equivalent to

\begin{equation*} \bigwedge_{i=1}^n (\{P\} p_i \{Q\}) \end{equation*}

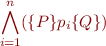
Note: the rule also applies to infinite union of paths (e.g. generated by loops).

Three Approaches to Generate Verification Conditions

Three equivalent formulations of Hoare triple give us three approaches:

  1. compute meaning of $c$ as a formula, then check Hoare triple (compositional approach for verification-condition generation)
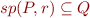  2. compute $sp(P,r)$ as a formula, then check entailment $sp(P,r) \subseteq Q$ (forward symbolic execution)
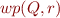  3. compute $wp(Q,r)$ as a formula, then check 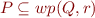$P \subseteq wp(Q,r)$ (backward symbolic execution)