LARA

Axioms and Inference Rules of Classical HOL

Axiom system that is sound (but necessarily incomplete with respect to standard semantics) is the following:

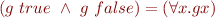  1. $(g\ true\ \land\ g\ false) = (\forall x. g x)$ (domain 'o' has only true,false as elements)
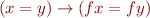  2. $(x=y) \rightarrow (fx = fy)$ (congruence)
  3. $(\lambda x.F_1)F_2 = F_1[x:=F_2]$ (beta reduction)
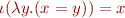  4. $\iota(\lambda y.(x=y)) = x$ (selecting element from $\{x\}$ gives $x$)

Inference rule:

\begin{equation*} \frac{C\ \ ; \ \ A=B} {C[A:=B]} \end{equation*}

which replaces one occurrence of $A$ in $C$ with $B$ (we cannot replace variables under $\lambda$)