This is an old revision of the document!
Asserts and errors for nice wp definition
We used assert(F) to express conditions that should hold.
Can we give executation semantics to assert?
assert(F) = irrecoverable error if  is false, terminates execution.
is false, terminates execution.
wp computes conditions sufficient for errors not to happen.
Postconditions are just asserts at the end of the program.
How to build a system with relations where at the same time
wp(assert(F),Q) = (F & Q) wp(assume(F),Q) = (F --> Q)
Then
wp(assert(false); assume(false),Q) = false wp(assume(false); assert(false),Q) = true
so cannot have 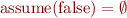 any more, otherwise both
any more, otherwise both
assert(false); assume(false) assume(false); assert(false)
would denote empty relations.
Error Variable and Good States
Introduce variable “error”. Good states are states where this variable has value zero. We write OK for the formula error=0.
We assume that the desired properties  satisfy
\[
\models P \rightarrow OK
\]
satisfy
\[
\models P \rightarrow OK
\]
Desired Rules for Weakest Preconditions
For all  such that
such that  , we would like the following to hold:
\[\begin{array}{l}
, we would like the following to hold:
\[\begin{array}{l}
\models wp(c,Q) \rightarrow OK \\ wp(c1 [] c2,Q) = wp(c1,Q) \land wp(c2,Q) \\ wp(c1 ; c2,Q) = wp(c1,wp(c2,Q)) \\ wp(havoc(x),Q) = \forall x.Q \\ wp(x=e,Q) = Q[x:=e] \\ wp(assume(F),Q) = (OK \land (F \rightarrow Q)) \\ wp(assert(F),Q) = (F \land Q)
\end{array}\]
We assume above that  is not the error variable.
is not the error variable.
Note: we wrote  in the weakest precondition of assume, but usually
in the weakest precondition of assume, but usually 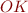 is implicit and we do not write it. We do not need it in other cases because it follows that right hand side implies
is implicit and we do not write it. We do not need it in other cases because it follows that right hand side implies 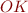 .
.
Relational Semantics that Fulfills These Rules
Let OK denote s(error)=0 and OK' denote s'(error)=0. We define:
![Equations \begin{eqnarray*}
R_c(\mbox{havoc(x)}) &=& \{(s,s') \mid OK \rightarrow (OK' \land \bigwedge_{{y \not\equiv x} s'(y)=s(y)) \} \\
R_c(\mbox{assert}\ F}) &=& \{(s,s') \mid (OK \land F(s)) \rightarrow s=s' \} \\
R_c(\mbox{assume}\ F}) &=& \{(s,s') \mid OK\ \rightarrow\ (F(s) \land s=s') \} \\
R_c(c_1 [] c_2) & = & R_c(c_1) \cup R_c(c_2) \\
R_c(c_1\ ;\ c_2) & = & R_c(c_1) \circ R_c(c_2)
\end{eqnarray*}](/w/lib/exe/fetch.php?media=wiki:latex:/img6f6269e1f750626a6c30bf69c3a5f18a.png)