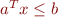TODO
Find out how to handle constraints among parameters (actually may be similar to SMT) [May not be tractable]
eg.
choose (x => a<=b<=c<=d<=e && x=a or b or .. or e)
should yield
if(x>=c)
{
if(x==c) return c
else if (x>=d){
if(x==d) return d
else if(x>=e){
if(x==e) return e
else throw new UnsatisfiableConstraint
}
else throw new UnsatisfiableConstraint
}
else throw new UnsatisfiableConstraint
}
else ...
Currently the algorithm will generate linear sized and linear time code(?), whereas the above example generates logarithmic time and linear size code
- Check if it is possible to use Voronoi Diagrams theory for Cell Decomposition (Sweeping algorithms)
Literature Survey on Integer and Rational Synthesis
Preliminary Definitions
Linear Rational Arithmetic formula
Polyhedron (always assumed convex)
Notations
Handling negations and strict inequalities
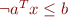 is replaced by
is replaced by 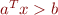 . Similar results hold for other constructs
So, to handle negations, one needs only to handle strict inequalities.
. Similar results hold for other constructs
So, to handle negations, one needs only to handle strict inequalities.
To handle the strict inequality 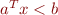 , we can add a slack
, we can add a slack  such that
such that  Then we maximize over
Then we maximize over  . If the maximum is 0, then we know that strict inequality cannot hold, else we just discard the value. Multiple non-strict inequalities can be handled this way??
. If the maximum is 0, then we know that strict inequality cannot hold, else we just discard the value. Multiple non-strict inequalities can be handled this way??
Alternatively, we use the notion of Not Necessarily Closed Polyhedra, for which the standard polyhedral operations can be implemented, with some modifications. Refer “Not necessarily closed polyhedra and Double Description method” not_necessarily_closed_polyhedra_and_double_description.pdf
Linear Rational Synthesis with disjunctions
It is assumed that the input formula is a quantifier free formula of the form:
Quantifiers, if any, as well as other operations such as  or
or  have been elminated during preprocessing
have been elminated during preprocessing
It is clear that every formula containing only linear constraints with conjunctions and disjunctions can be put into this form, if strict inequalities are included.
The elements of matrix A are all known rational values while those of b are unknown rational parameters which will become available at runtime. The aim is to generate code which uses the parameters and efficiently finds one satisfying assignment of values.
We shall refer to the parameters as “input variables” and to the variables whose values are to be found as “output variables”.
Motivation
Linear Disjunctive programs are powerful enough to represent Integer Linear Programming, Quadratic Programs( ?example) etc
Finding a solution to a problem is NP-hard, even without parameters.
?example) etc
Finding a solution to a problem is NP-hard, even without parameters.
With parameters, the problem is decidable, even if all the parameters are unknown.
We consider the case where the values in A are known, while those of b are parameters.
Even if none of the parameters of A were known, it is possible to generate the code for solving this problem using Gaussian Elimination for equalities and Fourier-Motzkin elimination for inequalities.
The problem is solvable and a polynomial sized code (wrt formula size), which executes in polynomial time, can be generated for Gaussian elimination, while doubly-exponential code(wrt formula size), which executes in  time, can be generated in Fourier-Motzkin elimination.
time, can be generated in Fourier-Motzkin elimination.
====Handling maximization problems====
A maximization problem
( : use a better example)
Expected kind of input for this program is (check)
: use a better example)
Expected kind of input for this program is (check)
choose( (x:Float) => x>=0 && x+y <= a && (y-x >= b || 2*x-y <= 7*c ) )
or, if arbitrary precision is required,
choose( (x:BigDecimal) => x>=0 && x+y <= a && (y-x >= b || 2*x-y <= 7*c ) )
and the expected output is a code giving a value for x satisfying these conditions. Clearly, many solutions are possible. The code will output only one. Here,
x= (a+7c)/3
and
x= (a-b)/2
are both valid solutions
For,
choose( (x:Float) => x>=0 && x+y <= a && (y-x >= b || 2*x-y <= 7*c ) )
and the expected output is a code giving a value for x satisfying these conditions. Clearly, many solutions are possible. The code is expected to output only one. Here,
if(a>=b) x= (a-b)/2 else if( a+7c >= 0) x= (a+7c)/3 else throw new UnsatisfiableConstraint
is a valid solution
Thus there are 2 parts to the problem:
- Identifying when the solution to a system exists in terms of the input variables
- Outputting a symbolic representation of the vector of output variables in terms of the input variables
Relation to Quantifier elimination
The solution to this problem can be achieved by quantifier elimination. (e.g. Ferrante-Rackoff elimination or the work described here: Quantifier Elimination for Real Arithmetic) Quantifier elimination is in fact projection, in our setting. However, we can use the geometric structure of the problem to achieve runtime efficiency and better worst-case bounds(???) on the elimination. Further, we wish to not only eliminate quantifiers, but to also give a witness function so that the values of the output function can be recovered. In this case, the elimination of quantifiers while also simultaneously storing the witness functions gives no advantage(?? is worse than) over calculating and minimizing the representation of the formula, and then applying the geometric projection operation on the resulting representation.
Polyhedra and unions of polyhedra
Polyhedra are defined as the set of solutions of the equation 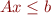 for
for 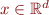 We consider 2 ways to represent Polyhedra.
We consider 2 ways to represent Polyhedra.
- H(alfplane)-representation : The polyhedron is represented as
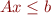 , i.e. the halfplanes which define it.
, i.e. the halfplanes which define it. - V(ertex)-representation: The polyhedron is represented as Vertices, Rays and Lines. i.e. the representation is the Minkowski sum: conv{v1,v2..,vn} + cone {w1, w2, … wn} + lin.space P
Where lin.space P is  such that
such that 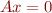
( Is lin.space P required?)
Is lin.space P required?)
Both these representations are unique if the Polyhedron is “full-dimensional”
The V representation is at worst exponentially larger than the H representation.
However, It is easy to intersect 2 H representations, whereas it is easy to find the convex hull of 2 V representations(simply take the union of vertices, rays and lines)
Operations on Polyhedra
Redundancy removal
This can be done by solving a linear program for each constraint to see if it is implied by the others
To check if a constraint 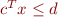 is redundant wrt the set
is redundant wrt the set 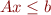
max $c^T x$ s.t. $A x \le b$ $c^T x \le d $ is redundant iff this maximum is less than d
To check if a constraint $c^T x = d$ is redundant wrt the set $A x \le b$ max $c^T x$ s.t. $A x \le b$ and min $c^T x$ s.t. $A x \le b$ $c^T x = d $ is redundant iff both of these are equal to d
The following heuristics can be applied to quickly remove redundancies:
- Kohler's rule
- Singular Determinant rule from practical_issues_on_projection_of_convex_sets.pdf
Intersection
To find the intersection in H-representation, we simply take the conjunction of the individual H-representations
Convex hull
To find the convex hull of 2 polyhedra, we do the following Consider the polyhedron $z=z_1+z_2$ $A_1 z_1 \le b_1$ $A_2 z_2 \le b_2$ Now, project out $z_1$ and $z_2$ to obtain the representation $A' z \le b'$ of the convex hull
However if the polyhedra are given in V-representation, we can simply take the union of their vertice and ray sets to get the convex hull
==Find if a hyperplane intersects the interior of a polyhedron== (determining points of contact is not required) : Solve a linear program
To check if $c^T x = d $ intersects $Ax \le b$, consider
max $c^T x $
s.t. $Ax \le b$
and
min $c^T x $
s.t. $Ax \le b$
If d lies between these values, it intersects otherwise it does not
OR
max $c^T x $
s.t. $Ax \le b$
$c^T x \le d $
This maximum equals d iff the hyperplane intersects the polyhedron
Using the Polyhedral domain
A standard technique, used by many polyhedral manipulation libraries, is to store both H and V representations, i.e. a double description of polyhedra.
For polyhedral manipulations, we may use a standard library such as PPL (Parma Polyhedra Library) PPL A list of available tools is present at Wikipedia
A survey of these representations is “Canonical representations of Polyhedra” by Fukuda et alcanonical_representations_of_polyhedra.pdf. Also, the book “Linear and integer Programming” by Schriver has some results and proofs.
Miscellaneous
Handling parameters
For
x+y+z<=a x,y,z=0 or a
we consider the polyhedron formed by taking all the variables (including the paramteres on the RHS) as a system.i.e.
x+y+z-a<=0 t= 0 or t-a=0 for t=x,y,z
Thus, we effectively treat this as a problem in a higher dimensional space
Simplification of Formulae
Simplification is tricky because it may be possible to have many representations for the same formula eg
x+y+z<=1 x,y,z= 0 or 1
is equivalent to
x=1,y=z=0 or y=1,x=z=0 or z=1,y=x=0 or x=y=z=0
Thus the first system produces 8 disjunctions while the second equivalent system produces only 4 (For n variables, it would be  vs
vs  )
We use the notion of cells to simplify formulae
)
We use the notion of cells to simplify formulae
Redundancy removal is also an important operation. The input given by the user is in the form of an intersection of Halfspaces, which may be redundant.
Cells
We partition the region into a union of a set  of convex polyhedra, each of which is called a “cell”.
of convex polyhedra, each of which is called a “cell”.
A cell is defined as any, bounded or unbounded, convex polyhedron.
A cell decomposition is a set of cells which satisfies:
- The cells are disjoint, except for their faces, i.e. the cells have disjoint interiors
- It has the same feasible region as

This is in slight contrast to the definition of cell complex found elsewhere in the literature, for example, Fukuda's Polyhedral FAQ, where each face of each cell is also included in the cell complex. We drop this condition.
We will call a cell decomposition “optimal” if no two cells in the decomposition are such that their union is a convex polyhedron. The optimal configuration is unique if the entire region is convex, otherwise many optimal decompositions can exist.
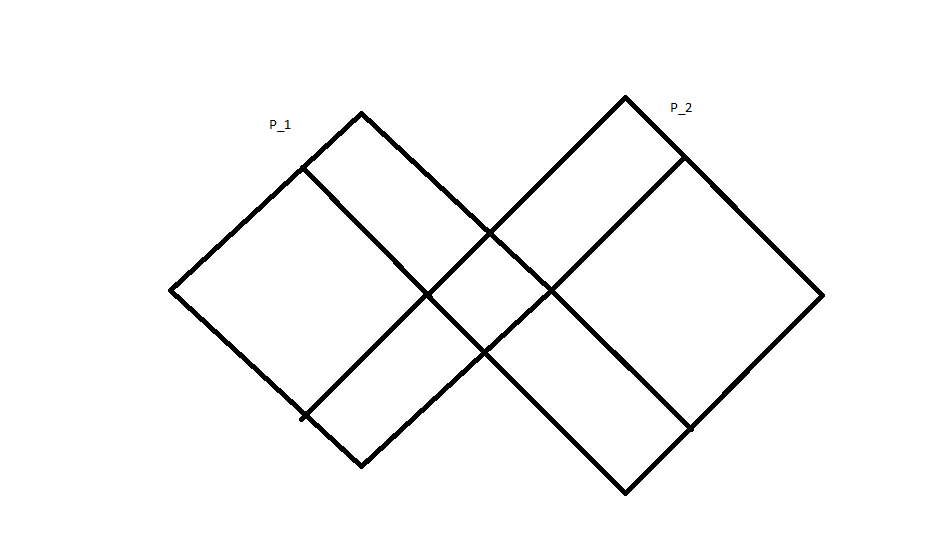
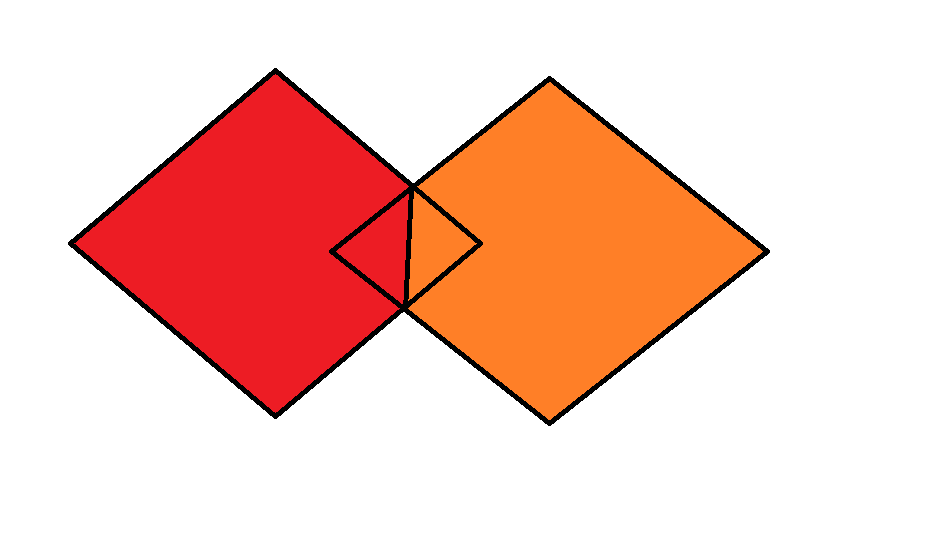
As Cell Decomposition is not unique, it can be achieved in different ways, we explain with respect to the 2 polyhedron case:
- We can consider all the constraints together and consider the set of generated regions (the size of this set will be exponential in the number of constraints – exact answer is ~ sum C(n+i,i)
 ). Thus the face of each cell will be one of the constraints of the system.
). Thus the face of each cell will be one of the constraints of the system.
=Naive Algorithm=
Consider all  possibilities for regions (i.e. taking each constraint and its negation).
possibilities for regions (i.e. taking each constraint and its negation).
Some will be rules out as unsatisfiable straightaway (Use an LP solver)
For the remaining regions, use a SAT solver to find out if it is implied by the constraints (or convert to DNF and check if it is implied)
Output the those regions which are implied by the formula as the cells.
The following algorithm has probably the same worst case complexity, but practical complexity
Pseudocode for generating cells for 2 polyhedra
Input:  and
and  in the form of constraint matrices
in the form of constraint matrices
Output: A list of Polyhedra as constraint matrices which gives a cell decomposition of 
Algorithm:
Let 
Let the constraints of  be
be 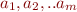
Repeat for i=1..m
For each 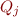 in
in 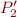
if  intersects the interior of
intersects the interior of 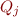 remove
remove 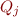 from
from 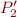 and add
and add 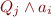 and
and 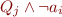 to
to 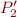
Return  as the cell decomposition
as the cell decomposition
Here,  should be taken to mean the closure of the negation, i.e.
should be taken to mean the closure of the negation, i.e. 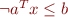 is
is 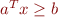
When the algorithm terminates, no constraint  of
of  intersects the interior of any polyhedron in
intersects the interior of any polyhedron in 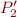 . By construction, no 2 polyhedra in
. By construction, no 2 polyhedra in 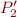 intersect. This operation will run in time exponential in the number of constraints in
intersect. This operation will run in time exponential in the number of constraints in 
Taken as formulae, this step is equivalent to : 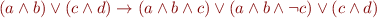 where both the disjuncts
where both the disjuncts 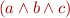 and
and 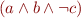 are non-empty. This non-emptiness is what is checked by the LP solver
are non-empty. This non-emptiness is what is checked by the LP solver
The algorithm to check if a polyhedron intersects solves a linear program, thus using the geometry of 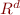 , which should(?) make this algorithm more powerful than blind manipulation of the constraints.
, which should(?) make this algorithm more powerful than blind manipulation of the constraints.
- Perhaps more efficiently, we can add additional constraints to create cells. We know that some coordinate must finally be projected away, so we may as well make cells perpendicular to that coordinate
However, this requires calculating the vertices of the polyhedron, which may be exponentially more than the number of constraints.
For example, consider the intersection of 2 polyhedra,  and
and  in
in  . If a point
. If a point 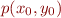 is a vertex of the intersection of
is a vertex of the intersection of  and
and  , we split
, we split  into
into 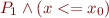 and
and 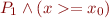 . The second one is not a polyhedron, but it can be represented as the part of
. The second one is not a polyhedron, but it can be represented as the part of  with
with 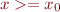 but not in
but not in  . Taking the representation of
. Taking the representation of  as the H representation, the decomposition of
as the H representation, the decomposition of  into cells can be found.
into cells can be found.
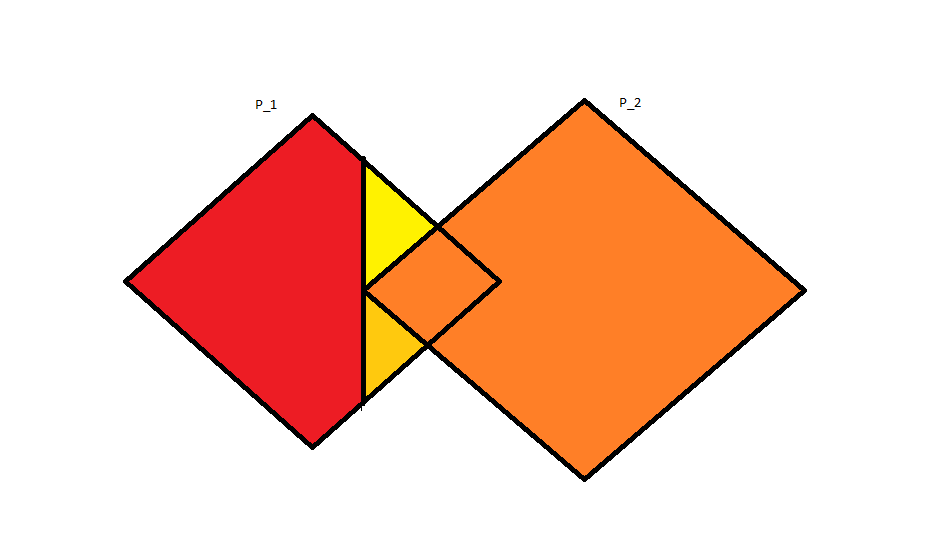
 clarify and resize diagram
clarify and resize diagram
Arguably, the best decomposition is this case is the following:
Finally, the union of convex polyhedra is now represented as a disjoint union of these cells. (And is represented as a list of polyhedra)
Algorithm for Cell Decomposition
Starting from the formula given as a tree where internal nodes are conjunctions and disjunctions and the leaves are linear rational constraints, we wish to output a cell decomposition for the feasible region of the formula. We create this decomposition exploiting the tree structure of the constraints. Our aim is to obtain an optimal cell decomposition for the set. This
Pseudocode
The algorithm simply generalizes the above procedure to conjunctions and disjunctions of polyhedra, and uses the tree structure to do so
Algorithm: CellDecompose Input: Linear Rational Arithmetic Formula as a Tree Output: A list of disjoint polyhedra which together cover the same region as the formula Assume: The internal nodes are only conjunctions and disjunctions, and the leaves are only polyhedral constraints (i.e. equalities and inequalities in matrix form)
If the node is a disjunction, take the pairwise i
If the node is a conjunction,
Main Algorithm
It is instructive to consider some important special cases of the algorithm are when the constraints consist of only conjunctions, only disjunctions, or disjunctive or conjunctive normal form.
Only conjunctions
We convert this set of constraints into a Polyhedron to potentially exploit the geometric structure.
In this case, we can apply Gaussian elimination to the equalities first. Then apply projection operations (such as Fourier Motzkin Elimination) to eliminate the output variables and thereby generate a polyhedron in only the input variables. The h representation of this polyhedron is also computed.
A solution exists given the parameters for this case iff the input variables satisfy all the inequalities implied by the polyhedron, and the corresponding values of input variables are given by the formulae derived from the input variables during the elimination.
So, the generated code is of the form
if( <H-representation matrix>*input_variables <= 0 )
output_variables = generatorMatrix * input_variables
Disjunctive normal form
Here each conjunction will be represented as a polyhedron, the aim is to find a minimal representation for the union of these polyhedra which is represented by the disjunctive normal form. We apply the cell decomposition method above to get a representation as a union of disjoint cells. Then we use each cell to generate the code for its polyhedra. After this, the code can simply be concatenated to give the final code eg.
if(<poly-1 condition>) output = poly1_mat * input if(<poly-2 condition>) output = poly2_mat * input
We can apply heuristics such as:
- Order the inputs by the size(volume) of the polyhedral regions they define
- The conditions can be represented as a decision tree and a reduced decision tree can be constructed
The Main algorithm is a slight generalization of the above algorithms
Pseudocode for the Main Algorithm
Procedure RationalSynthesis
Input: Formula  , List of input variables
, List of input variables  , List of output variables
, List of output variables 
Output: Code for a function which takes  as input and uses these values to compute values for variables in
as input and uses these values to compute values for variables in  such that
such that  is satisfied
is satisfied
Algorithm:
The input formula is assumed to be in the above normal form.
The Algorithm proceeds in three steps.
- Simplification The input formula is treated as representing a union of polyhedra given in the H representation. We apply the following techniques to eliminate redundant constraints:
- Split the polyhedral region into cells as described in the previous section. The number of cells can be exponential in the number of constraints in the worst case.
- Remove redundant constraints,i.e. constraints which are always implied by the remaining set of constraints. This can be done by calling an lp solver to check if a given constraint is redundant.
- Projection
The formula is represented as a list of disjoint polyhedra, i.e. as a disjunctive normal form. However, our representation is better because it the polyhedra are disjoint
We build the projection onto the set  by merging the projections of each cell.
by merging the projections of each cell.
If the formula $\phi = \phi_1 \vee \phi_2$, Then we must take the union of the projections of $\phi_1$ and $\phi_2$. This is just the union of the polyhedra representing $\phi_1$ and $\phi_2$ and simplify it.
If the formula $\phi = \phi_1 \wegde \phi_2$, then we consider pairwise the polyhedra that make up the $\phi_1$ and $\phi_2$ and, possibly, simplify this conjunction
If the formula $\phi$ is a linear constraint, i.e. $ A x \le b $ then, we use represent this solution as a polyhedron and project onto $O$ using Fourier-Motzkin Elimination.
- Code Generation
The intermediate representation in which the code is returned is a list of polyhedra in which the output variables have been projected out. As the representation at this stage is in fact just DNF, the code generation strategy is the same. However, the difference is that the polyhedra are now disjoint.
Given this list of polyhedra, we generate the decision trees for each polyhedron, using the H-representations. Then merge these decision trees. It is possible to make reduced decision trees.
For one polyhedron, the output is linear in the input variables
if(<condition on input variables>)
then output_variables = matrix * input_variables
Once the representation of the projection in terms of the input paramters has been obtained, It must be converted into a decision tree, i.e. if-then-else tree, from which code can be generated.
For code generation, we do the
Variations:
- The decision trees can be created and propagated upward in Step 2 instead of representing as polyhedra
- To solve conjunctions, we can use a constructive version of Helly's theorem to find a point in the intersection.
- Instead of projecting the whole set, project the convex hull of the set of inequalities, and output any extremal point of this projection.
- Block elimination instead of elminating variables one by one
Sources:
- Practical issues on the Projection of Polyhedral sets practical_issues_on_projection_of_convex_sets.pdf
- Disjunctive Programming by E. Balas disjunctive_programming.pdf
- Exploiting Sparsity in Polyhedral Analysis exploiting_sparsity_in_polyhedral_analysis.pdf – Optimizations for Fourier Motzkin
Notes about the implementation
For solving Linear programs, lp_solve java interface was used. (lp_solve)
Summer School on Convexity
The scribed notes of the Summer School have been stored at EPFL Summer School on Convexity And Spectral Algorithms
Helly's_theorem can be used, if the number of conjunctions is large as compared to the dimension, to efficiently decide if the intersection of sets is non-empty.
For example, to find if the intersection of a set  of convex sets with
of convex sets with  in
in  is nonempty, we consider every set of
is nonempty, we consider every set of  sets in
sets in  and consider their intersection. If the intersection of every set of
and consider their intersection. If the intersection of every set of  vertices is nonempty, then all the sets must intersect.
vertices is nonempty, then all the sets must intersect.
TODO: Traditional Proof of Helly's theorem is an existence proof, i.e. it proves that a point exists, but does not describe how to find the point. Find a constructive proof and see if it can be efficiently used.
Proof for a property of Convex Hull Extreme Point Algorithm
Consider the convex hull of a set  of (not necessarily disjoint) polyhedra. We prove that any extreme point of this convex hull is an extreme point of some polyhedron in
of (not necessarily disjoint) polyhedra. We prove that any extreme point of this convex hull is an extreme point of some polyhedron in  .
.
For simplicity, let  contain only polyhedra
contain only polyhedra  and
and  A point
A point  is called an extreme point if for any
is called an extreme point if for any 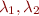 such that
such that  and
and 
Clearly, if a point is an extreme point of the convex hull and belongs to some polyhedron, then it is an extreme point of that polyhedron.
Consider a point 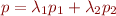 with
with  and
and 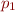 and
and  belong to some polyhedra in
belong to some polyhedra in 
Then, by definition, 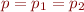 so that p belongs to some polyhedra in
so that p belongs to some polyhedra in  and is also an extreme point of that polyhedron.
and is also an extreme point of that polyhedron.
The above definition and the proof can be trivially extended to multiple polyhedra
Note: The extreme points of the convex hull are its vertices, if it is topologically closed.
The above result can help us quickly check for the existence of solutions. We can calculate the convex hull of the set of constraints and return any extremal point.