Type Soundness for Simply Typed Lambda Calculus
We apply the general method in Proving Safety Properties using Types to prove soundness of Simple Types for Lambda Calculus
Basic Notions
We consider the set of types  given by these two rules:
given by these two rules:
- int, bool

- if
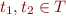 , then also
, then also 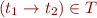
(In particular types cannot have any 'variables' or 'parameters' as in more complex type systems.)
Examples of types: int, bool, int→bool, int→int, (int→bool)→bool, …
What is a configuration used to represent program execution?
What is the initial configuration?
What is the reduction relation  ?
?
How to define the invariant  ?
?
How can we define  ?
?
- such that
 implies
implies  ?
? - what kind of expressions will error denote?
Well Typed Programs Have no Immediate Errors
Evaluation Preserve Types: Subject Reduction
We next show that the invariant  is inductive
is inductive
What does this mean?
What does  mean by Operational Semantics of Lambda with Letrec if we exclude rules for let/letrec
mean by Operational Semantics of Lambda with Letrec if we exclude rules for let/letrec
- primitive rule application in some context
![Math $C[(plus\ \overline n_1\ \overline n_2)] \leadsto C[\overline{n_1+n_2}]$](/w/lib/exe/fetch.php?media=wiki:latex:/img659601ce76337fc1163c2f6953545b7c.png) where
where  denotes the constant
denotes the constant 
![Math $C[(ite\ true\ e_1\ e_2)] \leadsto C[e_1]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgfc541c0858c711f4807b406b068dfd18.png)
![Math $C[(ite\ false\ e_1\ e_2)] \leadsto C[e_2]$](/w/lib/exe/fetch.php?media=wiki:latex:/img05a49dee17849686ee6ae51e25bdcfde.png)
- beta reduction:
![Math $C[(\lambda x:t.e_1)\ e_2] \leadsto C[e_1[x:=e_2]]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgcde4f26501cdf9badeba948060df399c.png)
 , we define
, we define 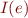 iff there exists a type
iff there exists a type  such that
such that 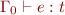
 x:t1. e2))
x:t1. e2))  , there is no environment
, there is no environment  and type
and type 
 for some
for some  .
.  for some type
for some type  of
of  .
. 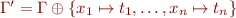 .)
.)  and
and  , then
, then 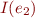
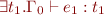 and
and  , then
, then 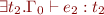
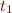 , can we guess what
, can we guess what  is?
is? 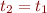
![Equation \begin{equation*}
\Gamma \vdash C[(plus\ \overline{n_1}\ \overline{n_2})]:t
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgb0b68622fe6e59fa161e9fef3c137528.png)
![Equation \begin{equation*}
\Gamma \vdash C[(\overline{n_1+n_2})]:t
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img8822d218dfd9b13d40c923272d6bad62.png)
![Math $\Gamma \vdash C[(plus\ \overline{n_1}\ \overline{n_2})]:t$](/w/lib/exe/fetch.php?media=wiki:latex:/imga8e3e90e775053ff832af00af75689e9.png) .
. 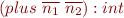 and this will be used in subsequent rules.
and this will be used in subsequent rules. .
. ![Math $C[(\overline{n_1+n_2})]:t$](/w/lib/exe/fetch.php?media=wiki:latex:/img3bf754da0083b6996218e5bda8637080.png)
![Equation \begin{equation*}
\Gamma \vdash C[(ite\ true\ e_1\ e_2)]:t
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img5eab5c0d2b462b890c6fbb4ebe727cd0.png)
![Equation \begin{equation*}
\Gamma \vdash C[e_1]:t
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img207850f3fad9daea3347e225eb98e57b.png)
![Equation \begin{equation*}
\Gamma \vdash C[(ite\ false\ e_1\ e_2)]:t
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imged1791a6b7e1e6233bb02ae0f5e34435.png)
![Equation \begin{equation*}
\Gamma \vdash C[e_2]:t
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img471d4d9db0c2ea19ce0b73e36895c6ef.png)
 can be derived only if
can be derived only if  and
and 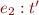 is
also derived (for a simple version of ite, we have that t' is int).
is
also derived (for a simple version of ite, we have that t' is int).
![Equation \begin{equation*}
\Gamma \vdash C[(\lambda x:t_1.e_1)\ e_2]:t
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img4880e59f6e36b47d0af1f2d766e938d0.png)
![Equation \begin{equation*}
\Gamma \vdash C[e_1[x:=e_2]]:t
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img5db1e1370a86bea83c0a2b3b5e504067.png)
![Math $\Gamma \vdash C[(\lambda x:t_2.e_1)\ e_2]:t$](/w/lib/exe/fetch.php?media=wiki:latex:/img80f0f681a1f1317ce890b02fcd43b0f2.png) , then
, then 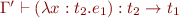 and
and  for some
for some  . Consequently,
. Consequently,
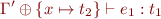
![Math $\Gamma' \vdash e_1[x:=e_2]:t_1$](/w/lib/exe/fetch.php?media=wiki:latex:/img2c34d20255ff00c0435d152cb042cda2.png) .
.
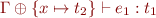 and
and  , then
, then ![Math $\Gamma \vdash e_1[x:=e_2]:t_1$](/w/lib/exe/fetch.php?media=wiki:latex:/imga1ddb3da10cc1de3d5c1093238a02f79.png) .
.
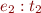 in the type derivation of
in the type derivation of ![Math $e_1[x:=e_2]:t_1$](/w/lib/exe/fetch.php?media=wiki:latex:/img0c5f783523030538bc1528f7d28b3ed5.png) whenever we would use
whenever we would use
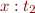 in the derivation of
in the derivation of 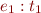 . The only subtle point is that we have
. The only subtle point is that we have  but we may need
but we may need
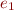 .
However, we can do capture-avoiding substitution by first renaming all bound variables within
.
However, we can do capture-avoiding substitution by first renaming all bound variables within  . For such renamed
. For such renamed  .
.