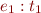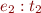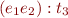Constraint-Based Type Checking and Inference
Motivation for Type Inference
Example:
% y:int. let ((f:int->int) = % x:int. x+3) in f (f (y+5))
Bottom-up type checking concludes:
y:int 5:int y+5:int x:int 3:int x+3:int (% x:int. x+3): int->int f:int->int f(y+5):int f(f (y+5)):int (% y:int. let ((f:int->int) = ...) : int->int
What if we have expression  without explicit type declarations:
without explicit type declarations:
% y. let (f= %x.x+3) in f (f (y+5))
Consider type constraints for %x.x+3. Assume
x:a x+3:b %x.x+3:c
where a,b,c are unknown types. Given that we know
3:int +:int->int->int
for x+3 to type check, i must be a=int and b=int. By abstraction rule then c = a→b = int→int. Therefore, f:int→int.
Similarly y+5 can be type checked only if y:int, and in that case y+5:int. Using type of f, we conclude f(y+5):int and f(f(y+5)):int. The entire expression  therefore has type int→int.
therefore has type int→int.
Bottom-Up versus Constraint-Based
We have seen bottom-up type checking
- obtain types for leaves
- propagate them to the root of syntax tree
- requires all lambda expressions to be typed
- what if some variables are undeclared?
- must propagate information in multiple directions
A more general, constraint-based approach:
- introduce a type variable corresponding to each tree node
- use type rules to describe constraints between variables
- solve constraints
Possible outcomes:
- no solutions: type error
- unique solution: program is type correct
- multiple solutions, either
- report umbiguity
- compute the most general type, allow expression use in many contexts
Lambda Calculus with Optional Types
E ::= v | E E | %d.E | (E:T) d ::= v:T | v T ::= int | boolean | T -> T
Note:
- declarations of types of variables are optional
- we can optionally annotate other terms with their concrete types
Type Constraints for Lambda Calculus
Rules for type constraints are like type checking rules, but:
- contain not only concrete types, but also types with type variables that denote unknown types
- contain constraints between types
Type inference process
- maintain in the environment a type variable for each bound variable
- introduce a fresh type variable
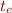 for each sub-expression
for each sub-expression 
- compute constraints between type variables
- solve type constraints
Constraints on type variables correspond to type checking rules
Variable Rule
If 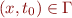 and
and 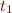 is the type introduced for an occurrence of
is the type introduced for an occurrence of  , then introduce constraints
, then introduce constraints 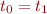
Abstraction Rule
When generating constraints for  , introduce a variable for
, introduce a variable for  for
for  and generate constraints for the body
and generate constraints for the body  in environment
in environment
 . To the resulting expression assign type
. To the resulting expression assign type  where
where 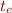 is the type variable for
is the type variable for  .
.
Application Rule
then 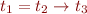
Type Annotation Rule
When expression  is explicitly typed
is explicitly typed  , then add
, then add 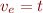 to constraints, where
to constraints, where 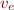 is variable for expression
is variable for expression 
Solving Type Constraints
Type constraints have the form  where
where  are type expressions containing:
are type expressions containing:
- ground (primitive) types int, boolean
- type variables
- function arrow constructor
Such constraints can be solved using Unification
- two types are equal iff variables can be instantiated to obtain same abstract syntax tree for types