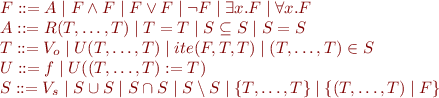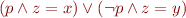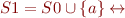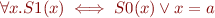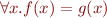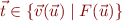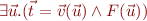First-Order Logic with Sets and Update Expressions

Claim: we can add update operations, a well as operations of set algebra on sets and relations to first-order logic. These constructs do not change the expressive power and can be eliminated. Result is a first-order logic formula.

Syntactic extension of FOL with if-then-else, function update, sets.

If-Then-Else

ite(p,x,y) = if p then x else y

Function Update

f (a:=b)(x)

f ( (a,b) :=c)(x,y)

Sets

Set variables (not quantified).

Set operations $\cup$ , $\cap$ , $\setminus$ , $\{x,y\}$ .

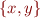Syntax Summary

$\begin{equation*}\begin{array}{l} F ::= A \mid F \land F \mid F \lor F \mid \lnot F \mid \exists x.F \mid \forall x.F \\ A ::= R(T,\ldots,T) \mid T=T \mid S \subseteq S \mid S=S \\ T ::= V_o \mid U(T,\ldots,T) \mid ite(F,T,T) \mid (T,\ldots,T) \in S \\ U ::= f \mid U((T,\ldots,T):=T) \\ S ::= V_s \mid S \cup S \mid S \cap S \mid S \setminus S \mid \{T,\ldots,T\} \mid \{ (T,\ldots,T) \mid F \} \end{array}\end{equation*}$