This is a sketch of the solution of SAV07 Homework 4
Part 1
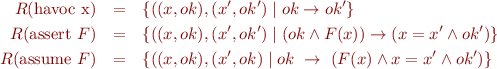
Then we have
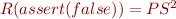 .
.
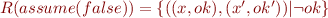
Then we have 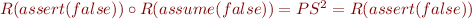 .
.
Note that we have 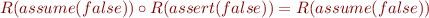 .
.
Basically, 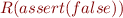 and
and 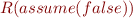 both act as a left zeros of
both act as a left zeros of  for the relations of the form
for the relations of the form 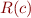 .
.
Part 2
It is easiest to use the definition of Galois connection given by  . The condition then reduces to
. The condition then reduces to

Both sides are equivalent to 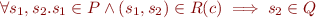 , that is, to the Hoare triple
, that is, to the Hoare triple  .
.
Part 3
 is not a partial order, it is merely a preorder.
is not a partial order, it is merely a preorder.
Part 4
Let  denote
denote 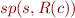 . We then have
. We then have 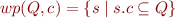 and the statement reduces to proving the equivalence between
and the statement reduces to proving the equivalence between
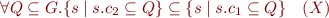
and
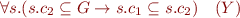
We prove both directions.
 : Let
: Let  . Take any
. Take any  such that
such that  . Then
. Then  , so
, so  . Therefore
. Therefore  .
.
 : Let
: Let  . Let
. Let 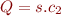 . Then
. Then  , so also
, so also  . Thus
. Thus  .
.
Part 5
Lemma:  .
.
 :
Let
:
Let  . Then
. Then 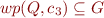 by construction of
by construction of  , so by definition of
, so by definition of  we have
we have  , i.e.
, i.e.  .
.
 :
Let
:
Let  . Then
. Then  . By monotonicity of wp, also
. By monotonicity of wp, also  , so
, so  .
.
![Math $c_1 \sqsubseteq c_2\ \rightarrow\ c_1 [] c_3 \sqsubseteq c_2 [] c_3$](/w/lib/exe/fetch.php?media=wiki:latex:/imgb2b9307f5bf39c544373630f69622484.png) :
Let
:
Let  . Then
. Then  , so by basic set theory
, so by basic set theory  .
.
assume(F)  skip
skip  assert(F), assert(F); assume(F)
assert(F), assert(F); assume(F)  assert(F), assume(F); assert(F)
assert(F), assume(F); assert(F)  assume(F) - follow from rules for computing weakest preconditions.
assume(F) - follow from rules for computing weakest preconditions.
Part 6
Suppose 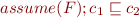 . Then by Part 5 we have
. Then by Part 5 we have
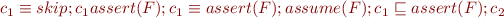
Suppose  . Then
. Then
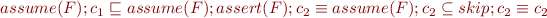
Suppose 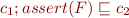 . Then
. Then
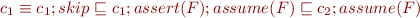
Suppose 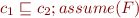 . Then
. Then
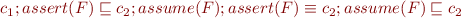
Part 7
By shunting rules in Part 6 we have  . By monotonicity properties in Part 5, we then obtain
. By monotonicity properties in Part 5, we then obtain ![Math $P \sqsubseteq P[c_1:=c_2]$](/w/lib/exe/fetch.php?media=wiki:latex:/img75e6271f9e7f2d927e80843ae18dac20.png) by structural induction.
by structural induction.