e
Deriving Propositional Resolution
We are extending the notion of substitution on formulas to sets of formulas by
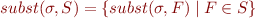
To make intuition clearer, we will next use quantification over potentially infinitely many variables and conjunctions over infinitely many formulas.
Proof System Based on Projecting Variables
We first derive a more abstract proof system and that show that resolution is a special case of it.
Key Idea
The condition that  is satisfiable is equivalent to the truth of
is satisfiable is equivalent to the truth of
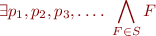
which, by changing the order of quantifiers, is:

By expanding existential quantifier, 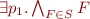 is eqivalent to
is eqivalent to
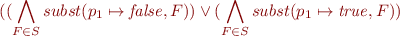
which, by distributivity of  through
through  is:
is:
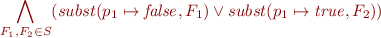
Let
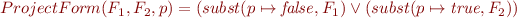
Then we conclude that  is equivalent to
is equivalent to  defined by
defined by
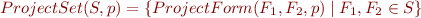
Projection Proof Rules
Above we justified the use of  as an inference rule. We write such rule:
as an inference rule. We write such rule:
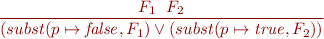
The soundness of projection rule follows from the fact that
for every interpretation  , if
, if  , then also
, then also 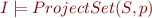 .
.
Applying the projection rule we obtain formulas with fewer and fewer variables. We therefore also add the “ground contradiction rule”

where  is formula that has no variables and that evaluates to false (ground contradictory formula). This rule is trivially sound: we can never
have a model of a ground formula that evaluates to false.
is formula that has no variables and that evaluates to false (ground contradictory formula). This rule is trivially sound: we can never
have a model of a ground formula that evaluates to false.
Iterating Rule Application
Given some enumeration  of propositional variables in
of propositional variables in  , we define the notion of applying projection along all propositional variables, denoted
, we define the notion of applying projection along all propositional variables, denoted  :
:

Completeness of Projection Rules
We wish to show that projection rules are a sound and complete approach for checking satisfiability of finite and infinite sets formulas. More precisely:
- if we can derive false from
 using projection rules and the ground rule, then
using projection rules and the ground rule, then  is unsatisfiable
is unsatisfiable - if
 is unsatisfiable, then we can derive false using projection rules and one application of the ground rule
is unsatisfiable, then we can derive false using projection rules and one application of the ground rule
Because we can derive false precisely when we have a ground false formula, these statements become:
- if
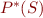 contains a ground contradiction, then
contains a ground contradiction, then  is not satisfiable
is not satisfiable - if
 is not satisfiable then
is not satisfiable then 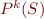 contains a ground contradiction for some natural number
contains a ground contradiction for some natural number  .
.
The first statement follows from soundness of projection rules. We next prove the second statement.
Suppose that  is not satisfiable. By the Compactness Theorem, a finite subset
is not satisfiable. By the Compactness Theorem, a finite subset 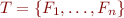 is not satisfiable.
Let
is not satisfiable.
Let 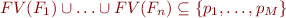 .
.
Consider the set
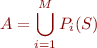
By definition of  , we can show that
, we can show that  contains a subset
contains a subset 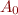 of ground propositional formulas equivalent to
of ground propositional formulas equivalent to
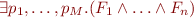
Because the above formula is contradictory, 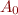 is a contradictory set of ground propositional formulas, so it contains a ground contradiction. Thus, we can set
is a contradictory set of ground propositional formulas, so it contains a ground contradiction. Thus, we can set 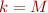 in the above theorem.
in the above theorem.
Improvement: Subsumption Rules
Note also that if 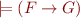 , where
, where  has been derived before, and
has been derived before, and  , then deriving
, then deriving  does not help derive a ground contradiction, because the contradiction would also be derived using
does not help derive a ground contradiction, because the contradiction would also be derived using  . If we derive such formula, we can immediately delete it so that it does not slow us down.
. If we derive such formula, we can immediately delete it so that it does not slow us down.
In particular, a ground true formula can be deleted.
Resolution as Projection
Recall Definition of Propositional Resolution.
Instead of arbitrary formulas, use clauses as sets of literals. The projection rule becomes
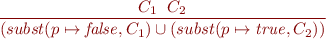
If  is a clause, then
is a clause, then

There are several cases:
Therefore, for clauses, projection (with some elimination of redundant conclusions) is exactly the resolution proof rule.
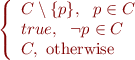

 , so it can be deleted
, so it can be deleted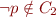
 , so it can be deleted
, so it can be deleted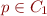 and
and 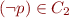 ,
, 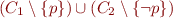 , as given by the resolution rule
, as given by the resolution rule