Transition System
We can represent programs as control flow graphs.
We can describe control-flow graphs as relations.
There are two ways to do this:
- using nested transitive closure for nested loops
- using only one transitive closure
The fact that we can use only one transitive closure corresponds to so called while theorem, which says that we can represent any program using only one loop.
Intuition: each loop iteration is making one step in control-flow graph.
- example nested loop: print all pairs (i,j) for 0
 i < j < 10
i < j < 10 - corresponding control-flow graph
- formula describing the control-flow graph
General form is a formula 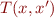
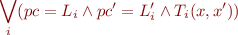
We describe a set of initial states by some formula 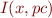 .
.
We call the above description of a program as 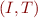 a transition system.
a transition system.
Essentially, transition system is just a set of states and a relation. Transition systems that come from programs usually have a notion of a program counter.
If we have a transition system, we can express all program properties using one set of good states, which are a complement of bad states.
We can represent an error state as a special node in CFG.
- An assertion checks a condition and jumps to error if the condition is false.
A system is safe it can never reach an error node in the control-flow graph.
In general, a correctness property is a description of a set of non-error states. We can specify it using a formula.
To show that a system is correct, we show
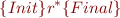
If  represents transition relation, this is the safety notion of correctness, which does not account for termination.
represents transition relation, this is the safety notion of correctness, which does not account for termination.
 here specifies the initial set of states, including program counter. Similarly for
here specifies the initial set of states, including program counter. Similarly for  .
.
We can define  , for example, as the set of non-error states. If we have a program counter location for an error, then we can take all states where program counter is not at an error location.
, for example, as the set of non-error states. If we have a program counter location for an error, then we can take all states where program counter is not at an error location.