A Temporal Logic Subset as WS1S Fragment

Overview

In linear temporal logic there is an implicit notion of time. Just like quantifiers update the environment with the variable over which they quantify, temporal operators update this implicitly named variable. The notion of implicitly named variables is also a feature of modal logics and appears in description logics that are fragments of FOL used in knowledge bases.

Temporal logic can be used to reason about programs.

Example: the following formula describes a protocol for opening file using openRead operation, which allows file to be read but not written:

globally(openReadInvoked $\rightarrow$ next( (isOpen $\land$ $\lnot$ (writeInvoked $\lor$ openReadInvoked) ) until closedInvoked)

( $\lnot$ isOpen) $\land$ globally ( ( $\lnot$ isOpen) $\rightarrow$ $\lnot$ (readInvoked $\lor$ writeInvoked) )

openReadInvoked	x
isOpen		x	x	…	x
writeInvoked
closedInvoked						x

Translation

If we assume that the time is given by a finite sequence (e.g. for terminating programs), we can translate temporal logic into WS1S.

Consider a temporal logic formula with operators next, globally, until, $\land$ , $\lor$ , $\lnot$ .

We fix a first-order variable $t$ and define translation function $\tau$ that maps a temporal logic formula into a WS1S formula that has $t$ as the free variable:

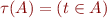$\tau(A) = (t \in A)$ (for a property $A$ , such as isOpen, openReadInvoked, …)
$\tau(F_1 \land F_2) = \tau(F_1) \land \tau(F_2)$
$\tau(F_1 \lor F_2) = \tau(F_1) \lor \tau(F_2)$
$\tau(\lnot F) = \lnot \tau(F)$
$\tau(F_1 \rightarrow F_2) = \tau(F_1) \rightarrow \tau(F_2)$
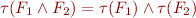
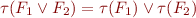
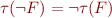
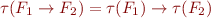
$\tau(\textbf{next} F) = \forall t_1.\ succ(t,t_1) \rightarrow \tau(F)[t:=t_1]$
$\tau(\textbf{globally} F) = \forall t_1.\ t \le t_1 \rightarrow \tau(F)[t:=t_1]$
$\tau(F_1 \mathop{\textbf{until}} F_2) = (\exists t_1. t \le t_1 \land \tau(F_2)[t:=t_1] \land (\forall t'. t \le t' < t_1 \rightarrow \tau(F_1)[t:=t_1]))$

Note: if we use finite sequences to denote the executions, then at some point all truth variables become false (at the end of the sequence), because all sets are finite. Usually in linear temporal logic one uses infinite words instead.

is complement of a set definable in WS1S? no, because complement of a finite set with respect to $\mathbb{N}$ is infinite

Note: The above translation shows decidability, but in practice there are more efficient methods specialized for LTL

Model Checking by Clarke, Grumberg, Peled

Translation into Automata

We can use either temporal logic over finite traces or full WS1S to describe properties. In any case, we can transform these properties into automata by using automata to decide ws1s.

Automaton for the example:

(open (read+write)* close)*