Deciding Exists-Forall Class
Theorem: Consider formula  of the form
of the form  where
where  is quantifier free formula of first-order logic with equality, without function symbols (only constants and relation symbols). Then there exists a structure in which the formula is true iff the formula is true in some structure whose domain is the set of constants in
is quantifier free formula of first-order logic with equality, without function symbols (only constants and relation symbols). Then there exists a structure in which the formula is true iff the formula is true in some structure whose domain is the set of constants in  .
.
Proof: Suppose that  is a model for
is a model for  . Let
. Let 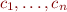 . Pick a substructure
of this model obtained by throwing away all elements other than the interpretation of constants
. Pick a substructure
of this model obtained by throwing away all elements other than the interpretation of constants 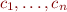 . We claim that we obtain a model for
. We claim that we obtain a model for  and keeping the definition of relations and predicates on
and keeping the definition of relations and predicates on 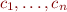 as in the structure. If we pick arbitrary values of
as in the structure. If we pick arbitrary values of  from the set
from the set 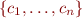 , then
, then  evaluates to true because it evaluated to true in the original structure. Therefore,
evaluates to true because it evaluated to true in the original structure. Therefore,  holds in the model for such structure.
End of proof.
holds in the model for such structure.
End of proof.
Note: there exists a counterpart of this theorem for function symbols, which ensures the existence of countable models for arbitrary first-order logic formulas. This is the Herbrand's theorem.
Example:
Consider the following formula:
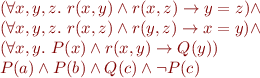
The formula is true iff the following formula over the domain 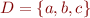 is true:
is true:
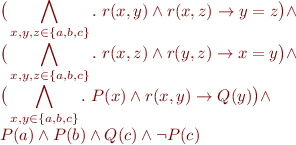
It suffices to search for the possible definitions of 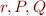 in domains of size 3 or less (it could happen that some of
in domains of size 3 or less (it could happen that some of 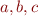 are equal).
are equal).
Thus we can find a model for the original formula.
Example: Prove that the following formula is valid:
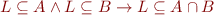
We check for counterexamples:
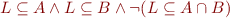
We express set operations using quantifiers:
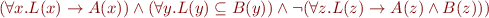
We propagate the negation:
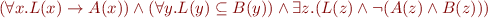
We replace the existential quantifier at the top level with a fresh constant  :
:
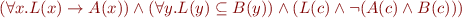
Now it follows that it suffices to check the formula on the domain 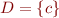 . The formula reduces to:
. The formula reduces to:
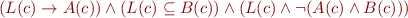
If we treat 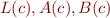 as propositional variables, we conclude that the formula is unsatisfiable. Therefore, the original formula is unsatisfiable.
as propositional variables, we conclude that the formula is unsatisfiable. Therefore, the original formula is unsatisfiable.