Determinization of finite state machine

For every finite state machine 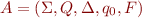$A = (\Sigma,Q,\Delta,q_0,F)$ there exists a deterministic finite state machine that accepts the same language.

This machine is given by $A_D = (\Sigma,2^Q,\Delta_D,\{q_0\},F_D)$ where

$\Delta_D = \{ (S,a,\Delta_{run}(S,a)) \mid S \subseteq Q, a \in \Sigma \}$
$F_D = \{ S \mid S \cap F \neq \emptyset \}$ .

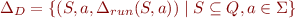
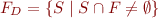The corresponding deterministic state machine maintains a set of states instead of just one state, and simultaneously transitions into all states that the original machine could reach from the current set of states.