Abstract Interpretation of a Transition System
Computing Invariants in a Transition System
Transition system is given by a set of initial states,  and one relation
and one relation  .
.
- relation
 specifies one step of a system
specifies one step of a system - we have seen that we can derive such relation from control-flow graph
- if we start from program that manipulates two integers
 , then
, then  will be relation on states of the form
will be relation on states of the form 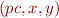 specifying the program point and the values of program variables
specifying the program point and the values of program variables
The reachable states of the system are 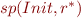 .
.
One important question is to check whether
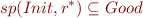
for some set of states  ; whether the reachable states are well-behaved (the completement
; whether the reachable states are well-behaved (the completement  are the Error states, so this is same as asking
are the Error states, so this is same as asking 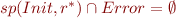 .
.
For this we seek  such that:
such that:
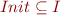
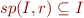 i.e.
i.e. 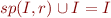

For every set  , define:
, define: 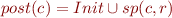
Then we are looking for  such that
such that 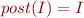 i.e. a fixpoint of
i.e. a fixpoint of 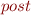 . We have in fact shown in homework that if the set of invariants is non-empty, then the least set such that
. We have in fact shown in homework that if the set of invariants is non-empty, then the least set such that 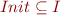 and
and 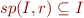 is in fact
is in fact 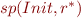 . This is the set of reachable states. Note that this set is the least fixpoint of
. This is the set of reachable states. Note that this set is the least fixpoint of 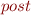 .
.
Suppose that 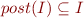 . This means
. This means
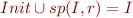
which implies both 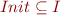 , and
, and 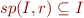 . It then remains to check
. It then remains to check  .
.
Approximating Invariants using a Lattice of Abstract Elements
We have seen that the set of possible invariants 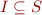 can be infinite.
can be infinite.
Therefore, we replace it with a smaller set  . Each element
. Each element  represents an entire set of states.
represents an entire set of states.
We formalize the notion represents using a concretization function 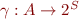 .
.
We then require  to be a lattice with order
to be a lattice with order  . Ideally, we can define lattice operations using corresponding operations on sets of states,
. Ideally, we can define lattice operations using corresponding operations on sets of states, 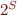 :
:
 iff
iff 
More generally, what we require is one direction of implication, which states that  is monotonic:
is monotonic:
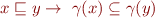
Observation: Suppose  iff
iff  and
and 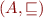 . Suppose
. Suppose 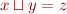 . Then
. Then  and
and  , so
, so
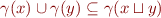
The equality need not hold in general.
Example: take  (the integers). Let
(the integers). Let  be the set of finite interval representations, extended with the set
be the set of finite interval representations, extended with the set  denoting all elements. Therefore, the abstract domain is:
denoting all elements. Therefore, the abstract domain is:
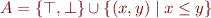
Define 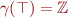 ,
, 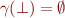 , and
, and  . We can prove that this order is a lattice.
. We can prove that this order is a lattice.
We can show that it holds that:

Note that, e.g. 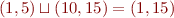 , so we have
, so we have
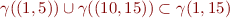
This illustrates one place where we use approximation to be able to work with the domain  instead of
instead of 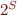 .
.
Is  an injective function?
an injective function?
Is  a surjective function?
a surjective function?
Approximating the Fixpoint
Our goal is now to approximate fixpoint using an element of the abstract domain  .
.
Remember 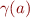 denotes the meaning of
denotes the meaning of  as the set of states.
as the set of states.
We will find  such that we still have
such that we still have 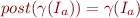 . It will not necessarily be the least invariant but we will have
. It will not necessarily be the least invariant but we will have
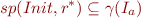
Thus,  will approximate the set of reachable states.
will approximate the set of reachable states.
We define 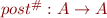 to be the abstract analog of
to be the abstract analog of 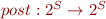 . We require the approximation to hold at every step, so the result of
. We require the approximation to hold at every step, so the result of 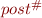 should represent at least the states represented by the concrete post. We thus require:
should represent at least the states represented by the concrete post. We thus require:
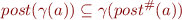
for all elements  of the abstract domain.
of the abstract domain.
Theorem: Let
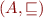 be a lattice
be a lattice 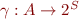 be a monotonic function
be a monotonic function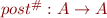 be such that
be such that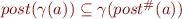 for all
for all  , and
, and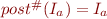 .
.
Then 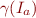 is a fixpoint of
is a fixpoint of 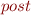 (and thus
(and thus 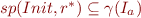 ).
).
Proof:
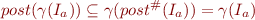
Thus 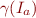 is a post-fixpoint of
is a post-fixpoint of 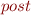 . Because
. Because 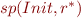 is the least fixpoint, we have
is the least fixpoint, we have 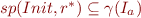 by e.g. Tarski's fixpoint theorem.
by e.g. Tarski's fixpoint theorem.
States and Domains in Analysis of Programs
When we construct a transition system from the program, we can take control-flow graph with statements and make program points part of the state, so if there is edge from  to
to  with command
with command  on the edge, we include into the relation
on the edge, we include into the relation  all tuples
all tuples
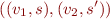
where 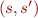 belong to the meaning of the command
belong to the meaning of the command  .
.
Because the number of program points is finite, we have two main kinds of choices when defining the abstract lattice  :
:
- flow-sensitive:
 has elements of the form
has elements of the form 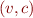 , specifying value for each program point, and is a product lattice of lattices for each program point. We define
, specifying value for each program point, and is a product lattice of lattices for each program point. We define
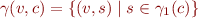
- flow-insensitive:
 has elements that ignore the program points. For example, we keep only one range for all possible values of program variables at all program points
has elements that ignore the program points. For example, we keep only one range for all possible values of program variables at all program points