Equivalence relation
An equivalence relation  is a binary relation on set
is a binary relation on set  (that is, a subset of
(that is, a subset of  ) that is reflexive, symmetric, and transitive, that is, the following three properties hold:
) that is reflexive, symmetric, and transitive, that is, the following three properties hold:
Given an equivalence relation  , we define the set of equivalence classes
, we define the set of equivalence classes 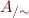 by
by
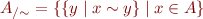
The equivalence classes of a non-empty set form a partition of  .
.
Conversely, given a partition 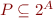 of set
of set  , the relation defined by
, the relation defined by
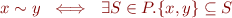
is an equivalence relation such that 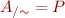 .
.


