Improving Symbolic Execution by using the Octagon Abstract Domain
Gautier Boucher Thomas Cellerier
The goal of our project is to improve systematic exploration by using symbolic execution. The principle is to delay concrete choice assignment as long as possible by using lazy execution.
Our project will focus especially on integers and will be based on Antoine Miné's paper (Octagons and relational analysis).
Our symbolic execution will be able to use of the form ±X±Y ⇐ c.
It is possible to deal with that kind of pattern in an efficient manner.
The constraints can be represented as a graph with variables as nodes and the constant c representing the octagonal constraint as the weight of the edges.
This graph has a small memory footprint as it can be represented efficiently as a n² matrix with n the number of variables in the program.
Furthermore it is possible to see if there is a solution effeciently.
With this method, getInt choices can be delayed.
Report
Abstract
Our work is based off on the article from Antoine Min\'{e} from ENS called The Octagon Abstract Domain.
It presents a new way to do static analysis on numbers by using octagons to represent constraints rather than intervals.
Octagons can be used to represent constraints of the type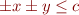 
where 
and 
are variables and 
a constant belonging to the same domain.
The objective of our project was to implement these techniques using octagons and integrate those with our symbolic execution interpreter from the previous exercises.
Contents
You can find our full report here: Improving Symbolic Execution by using the Octagon Abstract Domain
The code for our project can be found here: Symbolic Execution with Octagons