Octagons and Relational Analyses
Intervals track possible values for each variable independently.
More complex analyses are relational: they track relations between different variables.
Example of usefulness: prove  in this program:
in this program:
X := 10
Y := 0
while X >= 0 {
X := X-1
if random() { Y = Y+1 }
}
What would interval analysis compute? At iteration  , we have
, we have ![Math $X \in [10-k,10]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgb509e8de6cfabf455de6a9c18f7f8789.png) ,
, ![Math $Y \in [0,k]$](/w/lib/exe/fetch.php?media=wiki:latex:/img878e5f3def0cca091d3474bd7dfb9512.png) . Although
. Although ![Math $X \in [0,10]$](/w/lib/exe/fetch.php?media=wiki:latex:/img24be0f42356739a5480a7b452410747f.png) stabilizes, the interval for
stabilizes, the interval for  does not converge. We must widen and obtain
does not converge. We must widen and obtain ![Math $[0,+\infty]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgea8bdcebe4c013cbe0d8457ead4def60.png) .
.
What loop invariant does proof of  need?
need?
Note: relational analyses can also track changes of variables. If we automatically insert at the beginning of each procedure
x0 = x
for each variable x, then tracking relation between x0 and x tracks the changes to x since the beginning of procedure.
Example:  means the value only increases.
means the value only increases.
Octagon Domain
For each pair of variables  ,
,  , potentially track constraints of the form
, potentially track constraints of the form
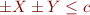
for some constant  .
.
It is a simpler and more efficient version of polyhedral domain, where constraints are general systems of linear equations of the form  for some matrix
for some matrix  and vector
and vector  .
.
Polyhedral domain uses the theory of linear arithmetic, whereas octagon domain uses theory of different logic, which is simpler and allows operations to be implemented using graph algorithms.
Reference
- A. Mine: The Octagon Abstract Domain (has 90 pages but is easy to read)
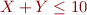 . Note it relates values of
. Note it relates values of