Procedure Contracts and Their Meaning
Example
var x : int
var wasEven : bool
proc even()
requires x >= 0
ensures (wasEven == (old(x) % 2 == 0))
{
if (x==0) {
wasEven = true;
} else {
x = x - 1;
odd();
}
}
proc odd()
requires x >= 0
ensures (wasEven == (old(x) % 2 != 0))
{
if (x==0) {
wasEven = false;
} else {
x = x - 1;
even();
}
}
What They Are
Procedure contract specifies:
- precondition: boolean expression that should be true in the initial state of the procedure whenever the procedure is invoked
- can refer to global variables, local variables (also parameters if there are parameters)
- postcondition: boolean expression that specifies
- in simpler case: condition that should be true whenever procedure ends
- in general: can also refer to relationship between initial and final state
- in general case it refers to initial and final global variables, parameters, and result
Meaning
Consider
var x, y;
proc p()
requires Pre(x,y)
ensures Post(x,y,oldx,oldy)
{ c }
The meaning is a relation. Which one?
What does it mean that the body c conforms to the relation?
Meaning in the example:
Meaning of
requires x >= 0 ensures (wasEven == (old(x) % 2 == 0))
is
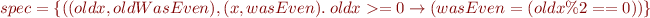
by renaming we have
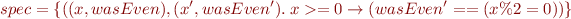
Since
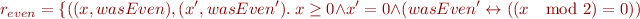
we have  . Note that the subset inclusion is strict: the specification allows arbitrary behavior in the case when the precondition is not met, and also does not restrict the final value of
. Note that the subset inclusion is strict: the specification allows arbitrary behavior in the case when the precondition is not met, and also does not restrict the final value of  .
.
Error States
If we introduce assertions and error states, then we have the implicit 'error' variable and we assume that the conjunct

is present in both 'requires' and 'ensures' clause. As a result, if an assertion can be violated for the given precondition, then error can become true in the final state, the relation inclusion will fail, and procedure does not meet the specification.
Contracts Expressed using Assertions
The meaning of the contract

can be expressed using this sequence:
x0 = x; y0 = y; assert(Pre(x,y)); havoc x; havoc y; assume(Post(x,y,x0,y0));
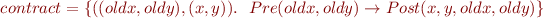
![Equation \begin{equation*}
[\![ c ] \! ] \subseteq contract
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img0116ad44e8ee0a1138e7ee8fd63d5515.png)