Labs 02

http://alloy.mit.edu

http://alloy.mit.edu/alloy4/tutorial4/

Checking FOL identities and counterexamples.

Formulas from Predicate Logic Informally have no counterexamples.

'Variations' such as:

$\begin{equation*} (\forall x. (P(x) \land Q(y))) \ \leftrightarrow\ ((\forall x. P(x)) \lor (\forall x. Q(x))) \end{equation*}$

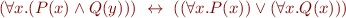
Relational identities

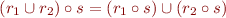
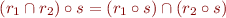
$\begin{equation*} (r_1 \cup r_2) \circ s = (r_1 \circ s) \cup (r_2 \circ s) \end{equation*}$

$\begin{equation*} (r_1 \cap r_2) \circ s = (r_1 \circ s) \cap (r_2 \circ s) \end{equation*}$

Sample Alloy Code

FOL

sig D { }
sig P in D { }
sig Q in D { }

// this shows no counterexample
//check { (all x:D|  (x in P) and (x in Q)) =>  (all x:D| x in P) and (all x:D| x in Q) }

// this shows counterexample
check { (all x:D|  (x in P) or (x in Q)) =>  (all x:D| x in P) or (all x:D| x in Q) }

Relations

// declaring binary relations r1,r2,s on A
sig A {
  r1 : set A,
  r2 : set A,
  s : set A  
}
// no counterexamples here:
// check { (r1 + r2).s = (r1.s + r2.s) }

// a counterexample here:
// check { (r1 & r2).s = (r1.s & r2.s) }