LARA

Example of using propositional resolution

Prove a tautology from examples in this lecture, e.g. left-to-right direction of

\begin{equation*} ((p \rightarrow q) \land\ ((\lnot p) \rightarrow r)) \leftrightarrow ((p \land q)\ \lor\ ((\lnot p) \land r)) \end{equation*}

Left to Right

Initial formula:

\begin{equation*} ((p \rightarrow q) \land\ ((\lnot p) \rightarrow r)) \rightarrow ((p \land q)\ \lor\ ((\lnot p) \land r)) \end{equation*}

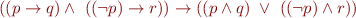
Negation of the formula:

\begin{equation*} ((p \rightarrow q) \land\ ((\lnot p) \rightarrow r)) \land \lnot ((p \land q)\ \lor\ ((\lnot p) \land r)) \end{equation*}

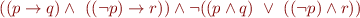
Eliminate implication:

\begin{equation*} ((\lnot p \lor q) \land\ (p \lor r)) \land \lnot ((p \land q)\ \lor\ ((\lnot p) \land r)) \end{equation*}

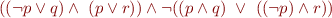
Negation normal form:

\begin{equation*} (\lnot p \lor q)\ \land\ (p \lor r)\ \land\ (\lnot p \lor \lnot q)\ \land\ (p \lor \lnot r) \end{equation*}

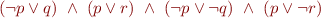
Set of clauses:

\begin{equation*} \{\lnot p, q\},\ \{p, r\}, \{\lnot p, \lnot q\},\ \{p, \lnot r\} \end{equation*}

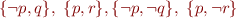
Apply systematically resolution

  • for each propositional variable
  • for each pair of clauses

Right to Left

Initial formula:

\begin{equation*} ((p \land q)\ \lor\ ((\lnot p) \land r)) \rightarrow ((p \rightarrow q) \land\ ((\lnot p) \rightarrow r)) \end{equation*}